Behavioral Bias Bingo — Ellsberg / Allais paradoxes: choice under uncertainty

Human beings crave certainty and loath ambiguity. People naturally gravitate towards the “sure thing” versus another option where the outcome is uncertain. Sometimes this is true even when the uncertain path may have huge upside.

Take William Orton, who was the President of Western Union in the 1860s. Many credit him with the worst business decision in history, a decision he made when faced with uncertainty versus a more certain path available to him.

When Orton was running Western Union, it was a business focused on business communications that tended to be short, and where reliability of transmission was paramount. When Alexander Graham Bell pitched Orton on the idea of an “acoustic telegraph,” Orton dismissed the idea, since he viewed it as inconsistent with the required fundamental attributes of the telegraph business; it was too radical an innovation, too difficult to commercialize.

Bell’s invention eventually became, of course, the telephone, arguably the most significant technological innovation of the 19th century. Orton fell victim to risk aversion. He was perhaps influenced by the “certainty effect,” which has been explored by academics.

Are you an effective decision maker? If you are like most people, you likely have a clear head when making choices under explicitly commutable risks (i.e., risks that can be exchanged for other risks), but may become less decisive when dealing with unknown risks and ambiguous situations. Today we present three games to test how you make choices under uncertainty.

Game 1: Ellsberg paradox

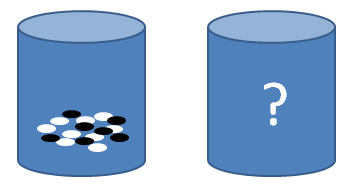
The Ellsberg paradox is a famous example that highlights risk aversion. If you are not familiar with the details, let’s first look at the figures below.

There are two urns, and each contains 100 balls. The left urn contains 50 black balls and 50 white balls, and the right one contains white and black balls in an unknown proportion.

You have a bet to make. A ball will be randomly drawn from one of the two urns, and in each numbered case below (numbered 1-4) you must make a choice between choice A, and choice B, or you can choose to be indifferent between the choices.

1. Do you bet that: A) a black ball will be drawn from the left urn, or B) a white ball will be drawn from the left urn?
2. Do you bet that: A) a black ball will be drawn from the right urn, or B) a white ball will be drawn from the right urn?
3. Do you bet that: A) a black ball will be drawn from the left urn, or B) a black ball will be drawn from the right urn?
4. Do you bet that: A) a white ball will be drawn from the left urn, or B) a white ball will be drawn from the right urn?

Pic source unknown. Game source: http://shookrun.com/bf/bfaversiontoambiguity.htm

If you are like most people, you will choose: 1. indifferent, 2. indifferent, 3, A, and 4. A. Let’s examine each of these choices in turn.

Choices 1 and 2 seem straightforward. You will not necessarily better off by betting on either black or white, if you’re choosing from only the left urn, or only the right urn. With the left urn, it’s a 50/50 bet, hence there’s no reason to prefer one over the other, and with the right urn, well you just don’t know the mix of black and white so it doesn’t make sense to choose one here either.

Choices 3 and 4 also seem to make sense independently. In both cases, you will prefer choosing from the left urn, where the odds are 50/50, rather than choosing from the right urn, which could be all black, all white, or some mix of the two.

Here is the paradox.

Imagine there is a third party, who is ignorant as to your knowledge of the contents of the right and left urns. This third party wants to try to assess your views of the probabilities by considering how you answered the questions.

This third party knows from the last 2 questions that: 1) you think black/left is more likely than black/right, and 2) you think white/left is more likely than white/right.

But these cannot both be “more likely” simultaneously. They cannot both be true. This is an impossibility, as your subjective probabilities sum to something greater than one for the left urn. Therefore, choosing A as the answer for both case 3 and 4 conveys no information about the underlying probabilities in these cases. This third party can’t make any judgments about the actual probabilities based on your answers.

Game 2: the Allais paradox

The Ellsberg paradox highlights our natural aversion to risk. The Allais paradox demonstrates what is known as the “certainty effect,” whereby when a certain outcome is available, it enhances this risk aversion.

Let’s look at the two cases below:

• Case I: Uncertainty versus Uncertainty, which do you choose?

A: $100 million with a probability of 11%, or $0 with a probability of 89%.
B: $500 million with a probability of 10%, or $0 with a probability of 90%.

• Case II: Certainty versus Uncertainty, which will you choose?

C: $100 million with a probability of 100% certainty.
D: $500 million with a probability of 10%, or $100 million with a probability of 89%, or $0 with a probability of 1%. 

In case I, most people choose B, since B has higher expected return than A. In a situations with one uncertainty versus another uncertainty (i.e., different degrees of risk), people tend to maximize expected value.

However, In case II, most people choose C, even though the expected value is higher in D. Why? People prefer the sure thing, even when an alternative may offer a superior expected return. Although the extreme downside case of a $0 payout is highly unlikely, we would experience a lot of regret if we lost, especially knowing we had forgone a chance to win with certainty.

Applications in Finance:

The Ellsberg paradox shows us that can depart from rational decision-making, as informed by probabilities, since we are averse to ambiguity and avoid probabilities when they are difficult to assess. As Frank Zhang pointed out, in a 2006 paper:

…the degree of incompleteness of the market reaction increases monotonically with the level of information uncertainty, suggesting that investors tend to underreact more to new information when there is more ambiguity with respect to its implications for firm value.

How might this be reflected in the market? We might favor preferred stock, with a dividend stream that has payouts of specific, fixed amounts, over an investment in common stock with more ambiguous payouts, including dividend increases and appreciation potential, which is hard to assess. Such a preference may be unduly affected by our aversion to ambiguity, rather than by a strictly rational assessment of each security, leading us to make the wrong decision.

The Allais paradox demonstrates that when faced with a “sure thing,” we can sometimes overweight its value relative to other opportunities, since the possibility of downside outcomes is highly salient, and available to us. In other words, our concern about the possibility of a bad outcome is not consistent with its probability; we overweight the risks when certainty is an option.

Consider a tender offer from a firm. You bought the stock at $5, and it has traded up to $10, and today, the company offers to repurchase your stock for today’s $10. You have recently done valuation research suggesting that the intrinsic value of the firm is actually $15. Yet, because you have a “bird in hand,” an offer to buy out your entire position at the $10 price, you conclude that you want to sell. Why? I would be too painful to see the stock trade back down below $10 and to have to sell at such a lower price, when you could have sold it at $10, which is a “sure thing.” In this case, you would be overemphasizing the downside risk, and discounting your own research, since you have a certain outcome available to you, which is distorting your judgment.

Decision makers, like physicians, patients, equity investors, and so on, prefer certainty, rather than complexity and ambiguity. This sometimes causes many decision makers to choose options that contravene the expected utility of the problem. That is, the certainty Effect contributes to risk aversion and will lead people make choices that inconsistent with expected utility theory.

Further Resources:

• Ellsberg, D. (1961). Risk, ambiguity, and the Savage axioms. Quarterly Journal of Economics, 75, 643–669.
• Allais, M. (1953). “Le comportement de l’homme rationnel devant le risque: critique des postulats et axiomes de l’école Américaine”. Econometrica.21 (4): 503–546.