Introduction to Finance: Class 2

Discounted Cash Flow Valuation

What is a discounted cash flow valuation?

Discounted cash flow (DCF) is a valuation method used to estimate the attractiveness of an investment opportunity. DCF analysis uses future free cash flow projections and discounts them to arrive at a present value, which is then used to evaluate the potential for investment. If the value arrived at through DCF analysis is higher than the current cost of the investment, the opportunity may be a good one.

—Source

If you’d like more background information on DCF, feel free to check out Investopedia’s introduction which offers a lot more uses of the method, as well as its shortcomings. The website even offer a short video further explaining DCF here.

DCF Valuation Video

 · · · · ·
Key Concepts:

• Future Value and Present Value of Investments with Multiple Cash Flows
• Annuities and Perpetuities
• EAR vs. APR (Interest Rates)
• Amortized Loans

Future Value and Present Value of Investments with Multiple Cash Flows

Future Value

KEY POINTS:

• The FV of multiple cash flows is the sum of the FV of each cash flow.
• To sum the FV of each cash flow, each must be calculated to the same point in the future.
• If the multiple cash flows are a fixed size, occur at regular intervals, and earn a constant interest rate, it is an annuity (will be explained later on). There are formulas for calculating the FV of an annuity.

Finding the future value (FV) of multiple cash flows means that there are more than one payment/investment, and a business wants to find the total FV at a certain point in time. These payments can have varying sizes, occur at varying times, and earn varying interest rates, but they all have a certain value at a specific time in the future.

The first step in finding the FV of multiple cash flows is to define when the future is. Once that is done, you can determine the FV of each cash flow using the formula below. Then, simply add all of the future values together.

—Source

  · · · · ·

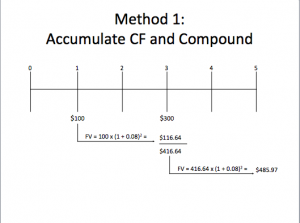
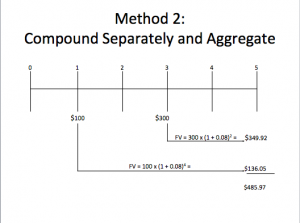
Suppose you plan to deposit $100 into a bank account in one year and $300 into the account in three years.  How much will be in the account in five years if the interest rate is 8%?

• Two ways to solve:

1. Accumulate cash flows and compound
2. Compound each cash flow separately and then aggregate

Present Value

 · · · · ·

You are considering an investment that will pay you $1,000 in one year, $2,000 in two years, and $3,000 in three years.  If you want to earn 10% on your money, how much would you be willing to pay for this investment?

• One way to solve:

1. Discount each cash flow separately and aggregate

  · · · · ·

• Suppose you will receive the following cash flows:
  • Year 1 CF = $100
  • Year 3 CF = $200
  • Year 5 CF = $300
• What is the value of the stream of cash flows today?
• What is the value of the cash flows at year 5?
• What is the value of the cash flows at year 3?
• Assume the discount rate is 7%

Annuities and Perpetuities

Annuity: finite series of equal cash flows that occur at regular intervals

• If the first payment occurs at the end of the period, it is called an ordinary annuity
• If the first payment occurs at the beginning of the period, it is called an annuity due

C = Cash flow per period
r = interest rate
t = time 

Annuity Example: Powerball

• On Christmas Eve, Rob and Tuesday Anderson of Kentucky won $128.6M in the Powerball Lottery.  The Anderson’s have a choice of receiving equal annual installments of $4.3M over 30 years or a lump sum of $64.3M.  If the appropriate discount rate is 5%, which option should the Anderson’s choose?

• PV of Lottery Annuity = C x [1 – 1 / (1 + r)^t] / r
• PV of Lottery Annuity = $4.3M x [1 – 1/1.0530] / .05
• PV of Lottery Annuity = $66.1M
• TAKE THE ANNUITY!

Finding the Annuity Payment

• Suppose you want to borrow $20,000 for a new car.  You can borrow at 1% per month (APR=12%).  If you take a 4-year loan, what is your monthly payment?

• PV = C x [1 – 1/(1 + r)^t] / r
• $20,000 = C x [1 – 1 / 1.01^(4×12)] / 0.01
• C = $526.02

Finding the Number of Payments

• You are a diehard Phillies fan, but you do not have the cash for World Series tickets.  So, you decide to use your credit card to buy two tickets, which cost $1,000.  Later you realize that you can only afford to make the minimum payment of $25 per month.  If the interest rate on the credit card is 2% per month, how long will it take to pay off the $1,000?

• Rearrange PV of annuity formula and solve for t
• t = ln(C / (C – PV x r)) / ln (1+r)
• t = ln(25  / (25 – 1,000 x 0.02)) / ln(1 + 0.02) = 81.27 months
• t = 6.77 years

Finding the Interest Rate

• You leave Drexel with $50,000 in student loans.  If you pay $450 per month for the next 15 years, what is the monthly interest rate on your loans?
• Either use your financial calculator to solve…
  • PV = -50,000
  • PMT = 450
  • N = 15 x 12 = 180
  • (CPT) I/Y = 0.59 → 0.59% / month
• Or, use trial and error

Perpetuity: infinite series of equal cash flow

• Present Value of a Perpetuity: PV = C / r
  • C is the per-period cash flow starting next period
  • r is the per-period discount rate

• You are considering buying preferred stock that pays a quarterly dividend of $1.50. If your desired return is 3% per quarter, how much would you be willing to pay?
  • PV = 1.50 / .03 = $50

Summary:

 · · · · ·

A. When you retire, you will require $3,000 per month to cover your living expenses.  If you can earn 0.75% per month in interest during retirement and you expect to need income for 25 years, how much do you need to have saved up in your account when you retire to meet these needs?

B. So, you need to have $357,485 in your bank account to meet your expenses during retirement.  Currently, your salary is $75,000 per year and not expected to increase until retirement.  After paying all of your expenses, you have disposable income of $15,000 per year.  If you are able to earn 8% per year on your money until retirement and you want to retire in 20 years, what percent of your disposable income must you put towards your retirement savings each year in order to fund your retirement needs?

EAR vs. APR (Interest Rates)

Effective Annual Rate (EAR)

• This is the actual rate paid (or received) after accounting for compounding that occurs during the year
• If you want to compare two alternative investments with different compounding periods you need to compute the EAR and use that for comparison

Computing EARs

• Suppose you can earn 1% per month on $1 invested today
  • What is the APR?  1% x 12 = 12%
  • How much are you effectively earning?
    • FV = $1 x 1.01^12 = $1.1268
    • EAR = (1.1268 – 1) / 1 = .1268 = 12.68%

• Suppose if you put it in another account, you earn 3% per quarter
  • What is the APR? 3% x 4 = 12%
  • How much are you effectively earning?
    • FV = $1 x 1.03^4  = $1.1255
    • EAR = (1.1255 – 1) / 1 = .1255 = 12.55%

Average Percentage Rate (APR)

• This is the annual rate that is quoted by law
• By definition APR = per-period rate times the number of periods per year
• Period rate = APR / number of periods per year

• You should NEVER divide the effective rate by the number of periods per year – it will NOT give you the period rate

Computing APRs

• What is the APR if the monthly rate is 0.5%?
  • .5% x 12 = 6%
• What is the APR if the semiannual rate is 0.5%?
  • .5% x 2 = 1%
• What is the monthly rate if the APR is 12% with monthly compounding?
  • 12% / 12 = 1%
• Can you divide the above APR by 2 to get the semiannual rate?
  • NO!!! You need an APR based on semiannual compounding to find the semiannual rate.

Things to Remember:

• You ALWAYS need to make sure that the interest rate and the time period match
  • If you are looking at annual periods, you need an annual rate
  • If you are looking at monthly periods, you need a monthly rate

• If you have an APR based on monthly compounding, you have to use monthly periods for your calculations, or adjust the interest rate appropriately if you have payments other than monthly 

 EAR vs. APR

EAR vs. APR: Comparing Rates

• You are looking at two savings accounts. One pays 5.25%, with daily compounding. The other pays 5.3% with semiannual compounding.  Which account should you open?

• First account:
• EAR = (1 + .0525/365)365 – 1 = 5.39%

• Second account:
• EAR = (1 + .053/2)2 – 1 = 5.37%

• Open first savings account with the higher EAR

 · · · · ·

A. Usury Bank (UB) is offering a loan with an APR of 36% with monthly compounding.  What is the effective annual rate of this loan?

B. First Predatory Bank (FPB) is offering a loan with the same EAR as UB, but quarterly compounding.  What is the APR on FPB’s loan?

C. You need to borrow $1000 to pay off some debts.  Larry the Loan Shark will give you the money you need in return for $1090 in three months.  Should you accept Larry’s offer, take out a three-month loan at UB, or take out a three-month loan at FPB?

Amortized Loans

The paying off of debt with a fixed repayment schedule in regular installments over a period of time. Consumers are most likely to encounter amortization with a mortgage or car loan.

—Source

Amortized Loan with Fixed Payment

• Each payment covers the interest expense; plus, it reduces principal
• Examples: mortgage, car loan, student loan

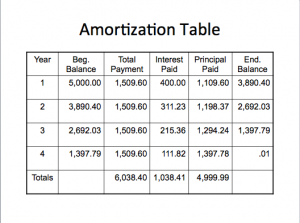
• Consider a 4-year loan with annual payments. The interest rate is 8% and the principal amount is $5,000
  • What is the annual payment?
    • $5,000 = C[1 – 1 / 1.084] / .08
    • C = $1,509.60

An amortization schedule is a chart showing a complete breakdown of periodic blended loan payments. It shows the amount of principal and the amount of interest that comprise each payment so that the loan will be paid off at the end of its term.

—Source

Wrap-Up

• Calculating FV and PV of investments with multiple cash flows is simply an application of tools developed prior
• Annuities and perpetuities are special cases of multiple cash flow investments and have closed-form PV formulas
• Use EARs to compare returns and APRs to calculate period interest rates

 · · · · ·

Solutions

1. 

• PV = $100/(1.07) + 200/(1.07)3 + 300/(1.07)5 =  $470.61
• FV5 = $470.61 x (1 + 0.07)5 = $660.05
• FV3 = $470.61 x (1 + 0.07)3 = $576.52

 
2. A

• PV of Annuity = $3,000 x [1 – 1 /(1+0.0075)25×12 ] / 0.0075
• PV of Annuity = $357,485

 
2. B

• FV of Annuity = $357,485 = C x [(1 + 0.08)20 – 1] / 0.08
• C = $7,811.84
• Save 52% (7,812 / 15,000) of disposable income each year

 
3. A

• EAR = (1 + 0.36/12)12 – 1 = 0.4258 → 42.58%

 
3. B

• APR = 4 x [(1 + 0.4258)1/4 – 1] = 0.3709 → 37.09%

 
3. C

• Larry the Loan Shark: $1,090
• Usury Bank: $1000 x (1 + 0.36/12)^3 = $1,092.73
• First Predatory Bank: $1000 x (1 + 0.3709/4)^1 = $1,092.73
• Better off asking Larry for the money

For more classes:

Education Series