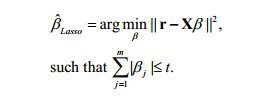In Search of Missing Risk Factors: Hedge Fund Return Replication with ETFs
- J. Duanmu, Y. Li, and A. Malakhov.
- A version of the paper can be found here.
- Want a summary of academic papers with alpha? Check out our Academic Research Recap Category!
- h/t to CXOAdvisory for bringing this to our attention
Abstract:
Properly considering all potential risk factors through tradable liquid portfolios in the context of a risk based factor model is paramount to quantifying the benefits of investing in hedge funds. We attempt to span the space of potential risk factors with exchange traded funds (ETFs). We develop a methodology of hedge fund return replication with ETFs based on cluster analysis and LASSO factor selection that overcomes multicollinearity among ETFs and the data mining bias. We find that the overall out-of-sample accuracy of hedge fund replication with ETFs increases with the number of ETFs available. This is consistent with our interpretation of ETF returns as proxies to a multitude of alternative risk factors that could be driving hedge fund returns.
We further consider portfolios of “cloneable” and “non-cloneable” hedge funds, defined as top and bottom in-sample R2 matches. We find superior risk-adjusted performance for “non-cloneable” funds, while “cloneable” funds fail to deliver significantly positive risk-adjusted performance. We conclude that our methodology provides value in both identifying skilled managers of “non-cloneable” hedge funds, and also successfully replicating out-of-sample returns that are due to alternative risk exposures of “cloneable” hedge funds, thus providing a transparent and liquid alternative to investors who may find these return patterns attractive.
Not a bad match:
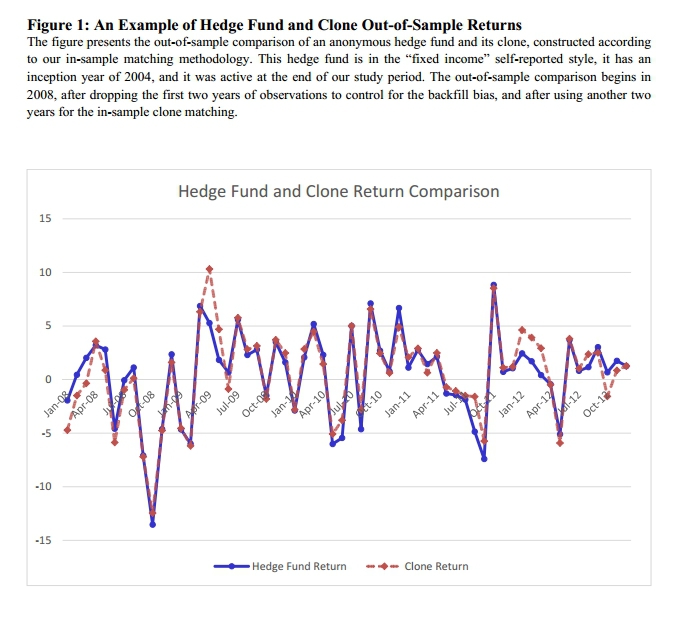
The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request.
The technique deployed is called a LASSO regression:
If the equation above blows your mind, here is a simple explanation of LASSO:
http://statweb.stanford.edu/~tibs/lasso/simple.html
In words, you’re optimization problem involves minimizing the sum of squares (standard linear regression), but the sum of the absolute value of the betas need to be under some number, t.
Here is a link to the source document:
http://statweb.stanford.edu/~tibs/lasso/lasso.pdf
About the Author: Wesley Gray, PhD
—
Important Disclosures
For informational and educational purposes only and should not be construed as specific investment, accounting, legal, or tax advice. Certain information is deemed to be reliable, but its accuracy and completeness cannot be guaranteed. Third party information may become outdated or otherwise superseded without notice. Neither the Securities and Exchange Commission (SEC) nor any other federal or state agency has approved, determined the accuracy, or confirmed the adequacy of this article.
The views and opinions expressed herein are those of the author and do not necessarily reflect the views of Alpha Architect, its affiliates or its employees. Our full disclosures are available here. Definitions of common statistics used in our analysis are available here (towards the bottom).
Join thousands of other readers and subscribe to our blog.