Prospect Theory Helps Explain Return Anomalies

The field of behavioral finance provides us with fascinating insights into individual investor behavior, including how individuals view risk, as well as the impact of those views on asset prices. Prospect theory plays a major role in explaining investor behavior. The theory, formulated in 1979 by Amos Tversky and Daniel Kahneman, describes how individuals make choices between probabilistic alternatives where risk is involved and the probability of different outcomes is unknown. Prospect theory is a challenge to the conventional expected utility theory which models the decision that perfectly rational agents would make. In contrast, prospect theory aims to describe the actual behavior of people. 

Prospect theory starts with the concept of loss aversion, the observation that people react differently between potential losses and potential gains. Thus, people make decisions based on the potential gain or losses relative to their specific situation rather than in absolute terms. Summarizing, faced with a risky choice leading to gains, individuals are risk-averse, preferring solutions that lead to a lower expected utility but with a higher certainty (concave value function). On the other hand, faced with a risky choice leading to losses, individuals are risk-seeking, preferring solutions that lead to a lower expected utility as long as it has the potential to avoid losses (convex value function). These examples contradict expected utility theory, which only considers choices with the maximum utility. ⁽¹⁾

The theory continues with a second concept, based on the observation that people in the tails of the distribution attribute excessive weight to low probability events and insufficient weight to events with high probability. For example, individuals may unconsciously treat an outcome with a probability of 99 percent as if its probability was 95 percent, and an outcome with a probability of 1 percent as if it had a probability of 5 percent. Under- and over-weighting of probabilities is distinct from under- and over-estimating probabilities, a different type of cognitive bias observed in the overconfidence effect.

New Literature

Nicholas Barberis, Lawrence Jin, and Baolian Wang contribute to the literature on prospect theory and the role it plays in asset pricing with their October 2019 study “Prospect Theory and Stock Market Anomalies.”

They begin by noting:

“Prospect theory is often implemented in conjunction with narrow framing, a phenomenon observed in experimental studies whereby, when an individual is thinking about taking on a new risk, he evaluates it to some extent in isolation, separately from his other risks. In the stock market context, this means that, when an investor is thinking about how much money to allocate to a particular stock, he focuses, at least in part, on the potential gains and losses in his holdings of the stock itself.” Nicholas Barberis, Lawrence Jin, and Baolian Wang

Nicholas Barberis, Lawrence Jin, and Baolian Wang

Narrow framing results from investors seeking short cuts to simplify complex problems. For example, it may be difficult for an investor to determine how a new risk interacts with pre-existing risks to affect overall wealth risk. As a consequence, investors evaluate the new risk, at least to some extent, as a stand-alone gamble.

The authors go on to explain:

“In an economy with prospect theory investors who engage in narrow framing, the price of an asset will depend in part on three asset characteristics: the volatility of the asset’s returns; the skewness of the asset’s returns; and the average prior gain or loss across investors holding the asset, a quantity known as the asset’s ‘capital gain overhang’. Nicholas Barberis, Lawrence Jin, and Baolian Wang

Nicholas Barberis, Lawrence Jin, and Baolian Wang

All else equal:

• Investors require a higher average return on more volatile assets: since these investors evaluate each asset to some extent in isolation, and since they are loss averse, they find assets with volatile returns unappealing.
• Investors require a lower average return on assets with more positively-skewed returns: since these investors focus on an asset’s own distribution of potential gains and losses, and since they overweight the tails of this distribution, they find assets with positively-skewed returns attractive.
• Investors require a higher average return on assets where they have larger prior gains.

Based on these observations they built a model incorporating all the elements of prospect theory, accounting for investors’ prior gains and losses in each risky asset. In their model, investor preferences have two components. The first is the traditional mean-variance preference specification; taken alone, it leads to the CAPM. The second embeds prospect theory and narrow framing. They then examined whether their model can explain 22 prominent asset pricing anomalies—the ones which have received the most attention from researchers. The model predicts returns depending on market beta, return volatility, return skewness, and capital gain overhang of stocks ranking by decile for each of the 22 anomalies. The objective is to determine if the model can explain the following 22 anomalies; idiosyncratic volatility; market capitalization; value; expected idiosyncratic skewness; momentum; failure probability; O-Score; net stock issuance; composite equity issuance; accrual; net operating assets; gross profitability; asset growth; return on equity; investment; maximum daily return; organizational capital; long-term reversal; external finance; short-term reversal; difference of opinion; and post-earnings announcement drift.

Barberis, Jin, and Wang noted the importance of their quantitative approach—depending on the anomaly, the three traits (volatility, skewness, and capital gain overhang) can predict different outcomes. Consider small-cap stocks. The returns of the typical small-cap stock are much more volatile than those of the typical large-cap stock. All else equal, this leads prospect theory investors who engage in narrow framing to charge a higher average return on small-cap stocks than on large-cap stocks, thereby helping to explain the size anomaly. However, the typical small-cap stock also has more positively-skewed returns, and a more negative capital gain overhang, than the typical large-cap stock. All else equal, these two factors lead prospect theory investors to charge a lower average return on small-cap stocks, thereby hampering the model’s ability to explain the size anomaly. The quantitative approach allows them to discover what the overall prediction of prospect theory for the size anomaly is, once all of these factors are properly combined, allowing one to see which, if any, trait dominates.

Findings

The study’s data sample covers the period 1963 through 2015. 

Following is a summary of their findings:

• The three characteristics, standard deviation, skewness, and gain overhang, are strongly correlated across anomaly deciles. If the typical stock in decile 1 for some anomaly has more volatile returns than the typical stock in decile 10 for that anomaly, it almost always also has more positively-skewed returns and a more negative capital gain. This holds for 21 of the 22 anomalies, with the only exception being post-earnings announcement drift.
• The model helps explain 13 of the 22 anomalies, in that it predicts a higher CAPM alpha for the extreme anomaly decile portfolio that actually has a higher alpha, empirically. These are the momentum, failure probability, idiosyncratic volatility, gross profitability, expected idiosyncratic skewness, return on equity, maximum daily return, O-score, external finance, composite equity issuance, net stock issuance, post-earnings announcement drift, and difference of opinion anomalies. The strongest results are for the first five.
• For each of the 13 anomalies, the typical stock in the extreme decile with the lower average return is more highly skewed, more volatile, and has a lower gain overhang than the typical stock in the other extreme decile. The greater skewness and lower gain overhang of the former stock leads investors to charge a lower average return on it, while its higher volatility leads investors to charge a higher average return on it. Quantitatively, the first effect dominates.
• There are seven anomalies where the model performs poorly—size, value, long-term reversal, short-term reversal, accrual, asset growth, and investment anomalies. The most notable failures are the size and value anomalies. For example, value stocks are more highly skewed and have a more negative capital gain than growth stocks. This leads prospect theory investors to charge a lower average return on value stocks. However, value stocks are also more volatile, leading investors to charge a higher average return on them. Quantitatively, the first effect dominates. The model, therefore, predicts a lower average return on value stocks, contrary to the empirical facts. In the case of the size anomaly, while stocks in the smallest decile are the most volatile, for which investors require a higher return, they also have positively-skewed returns and trade at a loss, which leads investors to charge a low average return on them. Their analysis shows the second effect overwhelms the first.

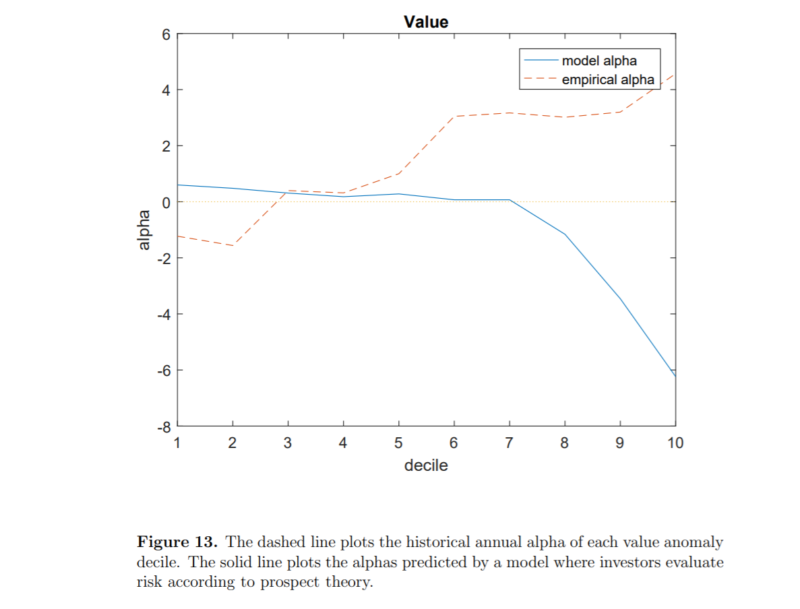
Barberis, Jin, and Wang noted an important issue regarding their model: “In making its predictions, our model assumes that investors have sensible beliefs: when pricing a stock, they are aware of the volatility and skewness of the stock’s future return distribution, and of its capital gain overhang. One possible explanation for our model’s poor performance on some anomalies is that investors have incorrect beliefs about stocks’ return distributions. We present some suggestive evidence from option prices that this is indeed the case for value stocks: investors appear to think that the returns on these stocks have similar skewness to the returns on growth stocks, even though, empirically, value stock returns are more highly skewed than growth stock returns. These incorrect beliefs may help explain our model’s counterfactual prediction about the average return on value stocks.”

Barberis, Jin, and Wang offer the following hypothesis for the cases where the model fails to explain returns well. “For some anomalies, the risk attitudes captured by prospect theory are not the primary driver of average returns. For example, for the value and long-term reversal anomalies, extrapolative beliefs about cash flows or returns may be more important than any aspect of preferences, while for the short-term reversal anomaly, liquidity-driven price pressure may be the most relevant factor.”

Summary

Barberis, Jin, and Wang make a major contribution to the literature on asset pricing. Their model, based on three elements of prospect theory, takes account of investors’ prior gains and losses and makes quantitative predictions about an asset’s average return based on empirical estimates of its beta, volatility, skewness, and capital gain overhang. The model helps explain 13 of the most prominent anomalies in finance. However, like all models, they are flawed, or wrong. They are not like cameras that provide a perfect picture of the world. If models were perfectly correct, they would be laws, like we have in physics. Instead, they are engines that advance our understanding of how markets work and prices are set.

You can benefit from their insights by incorporating their findings into your asset allocation decisions, avoiding stocks, and funds that buy stocks, from the 13 anomalies for which their model predicts low average returns, and buying stocks, and funds that buy stocks, for which their model predicts high average returns.  Investors who are subject to behaviors explained by prospect theory, and as a result buy stocks which have low expected returns, should take particular notice.