We’ve posted simulation and research-based studies on value and momentum. The evidence was pretty clear: never buy expensive stocks (Value) and ride winners and cut losers (Momentum). Another common “anomaly” is the low volatility anomaly. Empirical research here and here shows that low-volatility stocks (e.g. Beta or IVOL) earn higher risk-adjusted returns than portfolios of high-volatility stocks.
The research on high BETA stocks
Eric Falkenstein is the biggest proponent of the strategy on the blogosphere and there is a large following for the strategy:
Morningstar has 33 low-volatility funds in their database the last time we checked. We’ve done our own replication of these studies, and we’ve highlighted studies that question the results from low-volatility studies. Whether the low volatility anomaly is real is still up for debate. We ask if the low volatility anomaly stands up in the face of our simulation study framework. We examine 2 mainstream approaches to investing using volatility: 1) beta (BETA) and 2) idiosyncratic volatility (IVOL). We construct our simulated low-volatility portfolios, first based on BETA, and then on IVOL.
A PDF version of this is available here.
How Does Our Simulation Work?
Our two chosen volatility measures are constructed as follows:
- BETA is computed by regressing daily stock returns on value weighted CRSP over the last year (if forming portfolio on 1/31/13, we would compute the Beta using daily returns from 1/31/12-1/31/13). We only keep observations which have over 200 daily return observations. Beta is a measure of stock’s exposure to general market movements. We follow the basic methodology in Betting Against Beta.
- IVOL is the “the root mean squared error or the estimate of the standard deviation of the error term” of each stock. It’s a measure of the idiosyncratic risk of each stock. We follow the basic methodology in IVOL and the Cross-Section of Expected Returns.
Again, both BETA and IVOL are “flavors,” or different versions, of the volatility anomaly. We are curious to see how they do in our simulations, which give us a basis for comparing them against each other, and against value and momentum. We will review BETA and IVOL in turn, beginning with BETA. First, we break stocks down into 10 deciles from 1963 to 2013 based on BETA:
- For example, if there are 1000 stocks, stocks 1-100 go in the first decile (Low BETA); stocks 901-1000 go in the tenth decile (High BETA), and the stocks in between 101 and 900 go in their respective deciles.
Next, we conduct 1000 simulations of random 30 stocks portfolios drawn from either the “Low BETA” decile or the “High BETA” decile.
- An illustration of how this works: Image we have a monkey throwing 30 darts at the low BETA and high BETA stock universes every month for 50 years. For example, when the monkey is done throwing 50 year’s worth of monthly darts at our Low BETA stock universe, we will have 600 separate monthly portfolios (12 months*50 years) and will have made 18,000 (30 stocks*600 months) individual stock picks. This represents one simulation for Low BETA. So how did our monkey do? Maybe he got lucky, or maybe not, but one thing we know is his dartboard consisted of only Low BETA stocks. We will do 1000 such simulations for the Low BETA decile and another 1000 simulations for the High BETA decile. Now we have 1,000 50-year monkey investors throwing darts at the Low Beta dart board, and another 1,000 50-year monkey investors throwing darts at the High Beta dart board. In each case some monkeys will be lucky and some will be unlucky, but what will be interesting the comparison of how our 2 groups of monkeys did relative to each other on our two dart boards.
In order to do this, we calculate the performance statistics for each simulated strategy from 1963 to 2013. We calculate compound annual growth rates (CAGR), standard deviation, and maximum drawdown.
What Do the Returns to Low BETA and High BETA portfolios look like?
First, the distribution of CAGRs show that the Low BETA portfolios do generate higher returns than the High BETA portfolios. The results are strong, but not near as strong as the value and momentum simulations.
It would seem that a very lucky monkey throwing darts at the High Beta dart board has a chance to outperform an unlucky monkey throwing darts at the Low Beta dart board. This was not true for Value and Momentum, where there was essentially NO overlap. In other words, the vol anomaly is strong, but not as powerful as value or momentum.
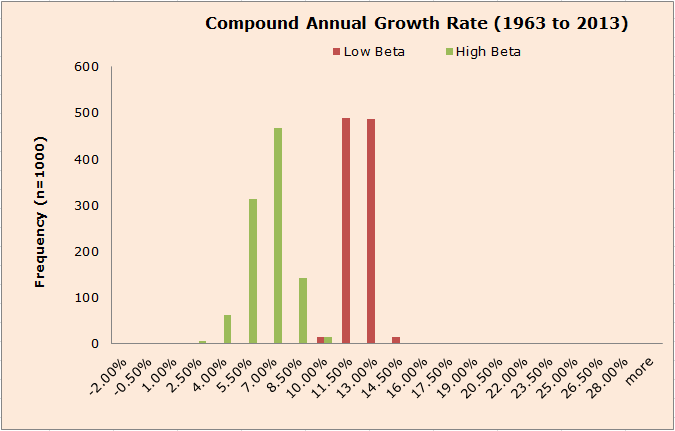
The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request.
Below is the table that outlines the simulation details.
| Bin | Low Beta | High Beta |
| -2.00% | 0 | 0 |
| -0.50% | 0 | 0 |
| 1.00% | 0 | 0 |
| 2.50% | 0 | 5 |
| 4.00% | 0 | 61 |
| 5.50% | 0 | 312 |
| 7.00% | 0 | 468 |
| 8.50% | 0 | 142 |
| 10.00% | 13 | 13 |
| 11.50% | 489 | 0 |
| 13.00% | 486 | 0 |
| 14.50% | 13 | 0 |
| 16.00% | 0 | 0 |
| 17.50% | 0 | 0 |
| 19.00% | 0 | 0 |
| 20.50% | 0 | 0 |
| 22.00% | 0 | 0 |
| 23.50% | 0 | 0 |
| 25.00% | 0 | 0 |
| 26.50% | 0 | 0 |
| 28.00% | 0 | 0 |
| more | 0 | 0 |
How About the Risks associated with investing in high BETA stocks?
Low BETA portfolios clearly have less volatility than high BETA portfolios. Standard deviation estimates are tightly bound, even across 1000 simulations.
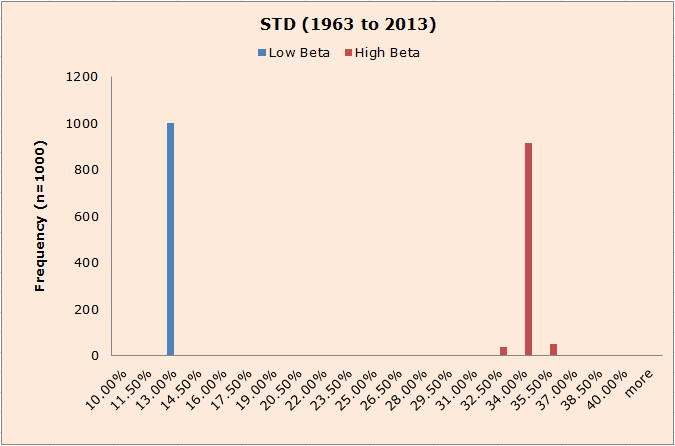
The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request.
Below is the table that outlines the simulation details.
| Bin | Low Beta | High Beta |
| 10.00% | 0 | 0 |
| 11.50% | 0 | 0 |
| 13.00% | 1001 | 0 |
| 14.50% | 0 | 0 |
| 16.00% | 0 | 0 |
| 17.50% | 0 | 0 |
| 19.00% | 0 | 0 |
| 20.50% | 0 | 0 |
| 22.00% | 0 | 0 |
| 23.50% | 0 | 0 |
| 25.00% | 0 | 0 |
| 26.50% | 0 | 0 |
| 28.00% | 0 | 0 |
| 29.50% | 0 | 0 |
| 31.00% | 0 | 0 |
| 32.50% | 0 | 36 |
| 34.00% | 0 | 917 |
| 35.50% | 0 | 48 |
| 37.00% | 0 | 0 |
| 38.50% | 0 | 0 |
| 40.00% | 0 | 0 |
| more | 0 | 0 |
As for maximum drawdowns, the evidence below suggests that Low BETA stocks protect the downside much better than High BETA stocks.
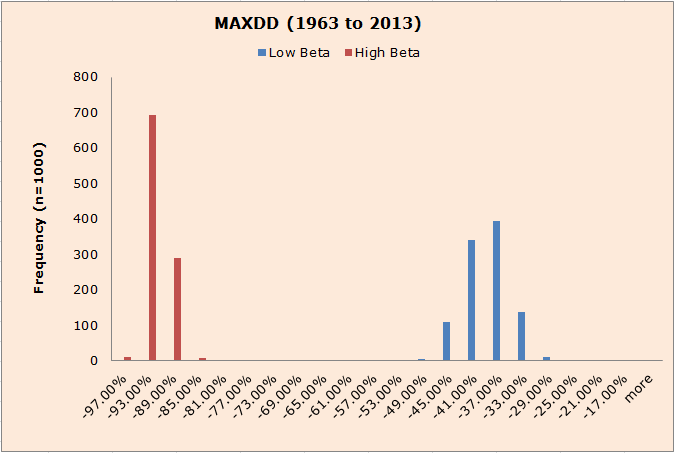
The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request.
Here is the table of observations:
| Bin | Low Beta | High Beta |
| -97.00% | 0 | 10 |
| -93.00% | 0 | 693 |
| -89.00% | 0 | 289 |
| -85.00% | 0 | 9 |
| -81.00% | 0 | 0 |
| -77.00% | 0 | 0 |
| -73.00% | 0 | 0 |
| -69.00% | 0 | 0 |
| -65.00% | 0 | 0 |
| -61.00% | 0 | 0 |
| -57.00% | 0 | 0 |
| -53.00% | 0 | 0 |
| -49.00% | 6 | 0 |
| -45.00% | 109 | 0 |
| -41.00% | 341 | 0 |
| -37.00% | 395 | 0 |
| -33.00% | 139 | 0 |
| -29.00% | 11 | 0 |
| -25.00% | 0 | 0 |
| -21.00% | 0 | 0 |
| -17.00% | 0 | 0 |
| more | 0 | 0 |
IVOL Robustness Tests
So Beta has some promise. What about an alternative approach to volatility based security selection? Academic research has considered idiosyncratic volatility, or IVOL, as another way to assess the low-volatility anomaly, generally. If IVOL results are strong, then we can conclude that volatility probably deserves closer scrutiny as a way to invest. IVOL asks a simple question: how good of a predictor is Beta for individually observed daily returns? If a stock’s Beta is 1.1 and the market goes up by 1.0%, will the stock always reliably move up by 1.1%? That is, is the Beta estimate a very accurate and reliable predictor with very little variation? Or it it noisy, and less reliable, with less predictive ability on a given day? IVOL represents a measure of the volatility that our explanatory variable, Beta, cannot explain. Formally, IVOL is the standard deviation of the residuals from a regression that uses Beta to estimate the relationship between a given asset and the market. IVOL tests serve as a robustness test on the volatility anomaly, and complements the study we did with BETA. Below are the charts/tables.
CAGR
- Low Ivol is the winner over High Ivol on CAGR, and the distance between two distributions is even larger than the split on BETA. Not bad. Not even the luckiest High Ivol investor monkey can beat the most unlucky Low Ivol investor monkey. Furthermore, return distributions for our Low Ivol investor monkeys are comparable to those achieved by our Low Beta investor monkeys.
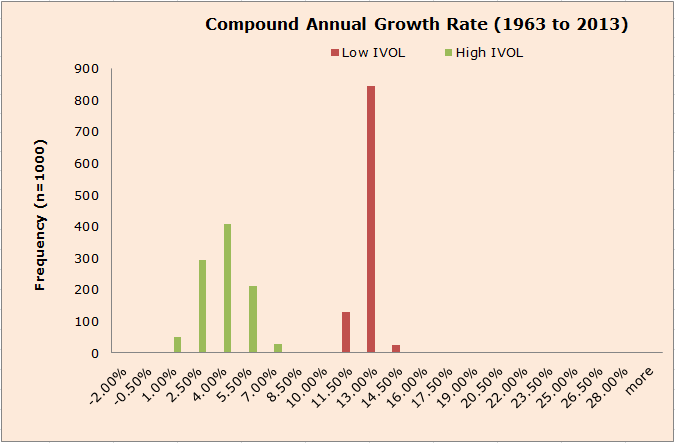
The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request.
Standard Deviation
- Volatility measures for Ivol are also similar to the BETA results.
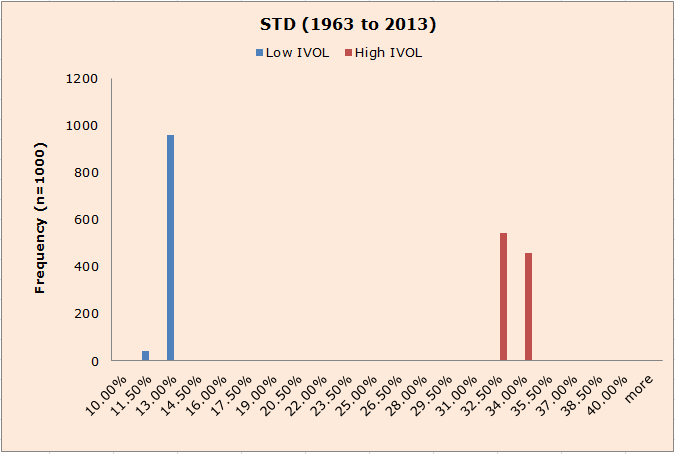
The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request.
Maximum Drawdowns
- MaxDD measures for Ivol are also similar to the BETA results.
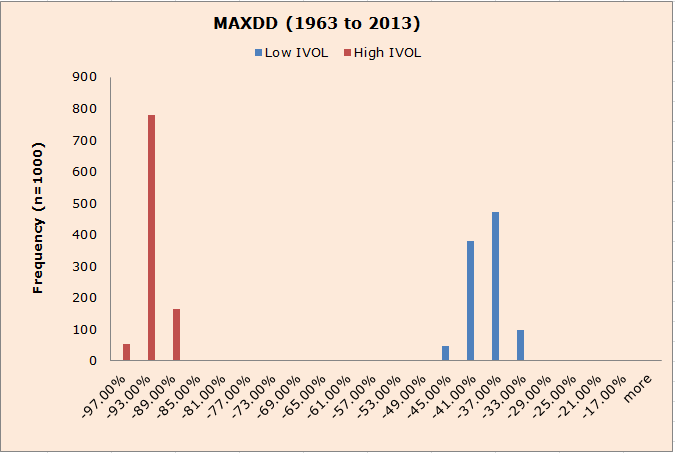
The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request.
Concluding our article on low volatility investing and high BETA stocks
Low volatility investing–either expressed via BETA or IVOL–does show promise. The simulation results are not as dramatic as those for value and momentum based strategies, but the results are certainly interesting. In a follow on study we will investigate the claim that low vol stocks might be value stocks with a different name. Stay tuned…
About the Author: Wesley Gray, PhD
—
Important Disclosures
For informational and educational purposes only and should not be construed as specific investment, accounting, legal, or tax advice. Certain information is deemed to be reliable, but its accuracy and completeness cannot be guaranteed. Third party information may become outdated or otherwise superseded without notice. Neither the Securities and Exchange Commission (SEC) nor any other federal or state agency has approved, determined the accuracy, or confirmed the adequacy of this article.
The views and opinions expressed herein are those of the author and do not necessarily reflect the views of Alpha Architect, its affiliates or its employees. Our full disclosures are available here. Definitions of common statistics used in our analysis are available here (towards the bottom).
Join thousands of other readers and subscribe to our blog.

