Warning: Stock and Bond Correlation Assumptions are Regime Dependent!

It ain’t what you don’t know that gets you into trouble. It’s what you know for sure that just ain’t so. — attributed to Mark Twain.

Mark Twain had some great insights. The quote above can apply to just about every aspect of life, including investing. This axiom is particularly relevant when one is making simplifying assumptions because you are implicitly stating that you know something for sure. However, oftentimes these accepted rules of thumb are actually far more complex (if not downright wrong) than is widely believed (see my articles on Target Date funds and safe withdrawal rates here and bonds providing crisis alpha here).

In this post, I will demonstrate how and why much of the conventional wisdom around stock and bond correlations is incorrect.

Are Stocks and Bonds Uncorrelated?

Stocks and bonds being uncorrelated is one of the most pervasive assumptions in finance. You have likely made this assumption yourself, either in the capital market assumptions in your financial plan, in the construction of your portfolio, or if you ever looked at stocks as being “risk on” and bonds as being “risk off”.

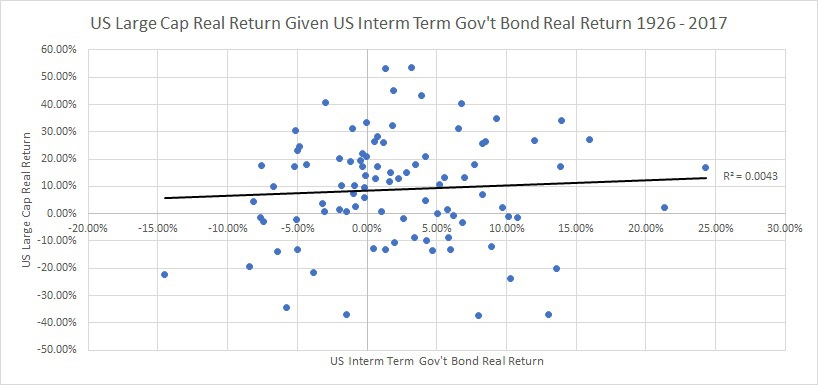
Using data from Ibbotson’s Stocks, Bonds Bills & Inflation from 1926 through 2017, I create a scatter plot of US Large Cap Stocks Inflation Adjusted Total Return vs. US Intermediate-Term Government Bonds Inflation Adjusted Total Return. In addition, I fit a regression line and show the r-squared for the relationship between the two data series.

Stock and bonds are uncorrelated. This statement is supported by historical data. As you can see, the regression line has an r-squared of .43%, or a correlation of 6.6%. In addition, one can see from the scatter plot that the results aren’t driven by a couple of outliers…there just doesn’t seem to be any relationship between the two time series.

Stock/Bond Correlations Differ by Regime

To fall further into the rabbit hole, we can ask – what happens if we look at the correlation by breaking the data into two parts 1) when bonds have had a negative return and 2) when bonds have had a positive return?

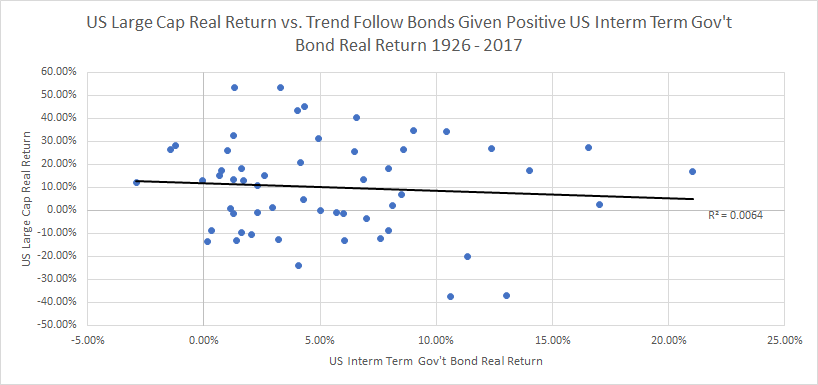
Positive bond return regime

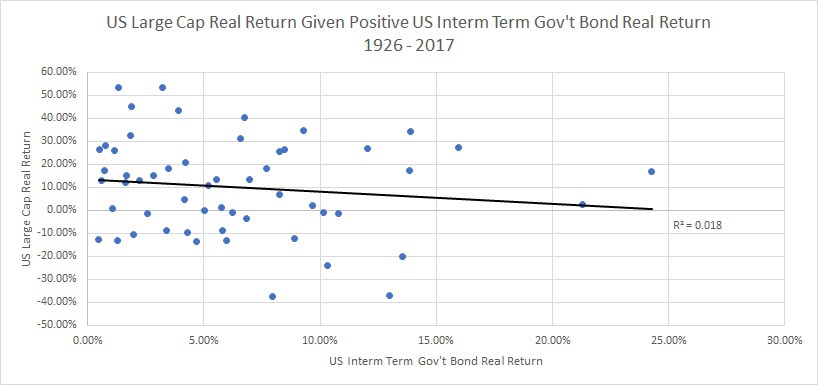
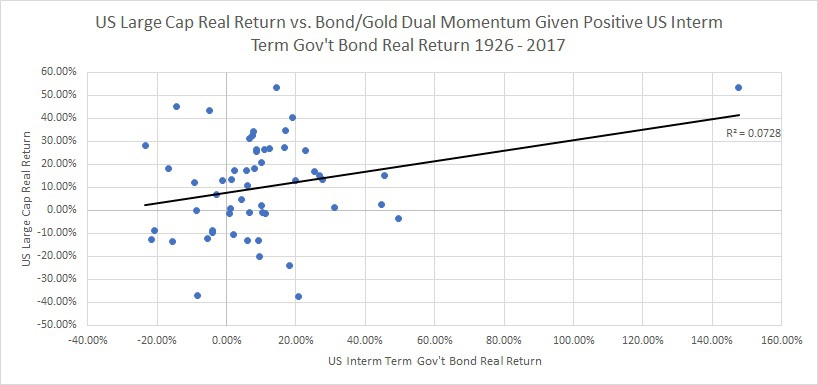
Below, I show the scatter plot for correlation of stocks and bonds, given that bonds had a positive real return:

What we see is that if bonds had a positive real return, stocks and bonds tended to have a slight negative correlation (negative 13%). This isn’t too dissimilar from the results looking at the whole time period and in addition.  This also makes the post-GFC negative correlation between stocks and bonds look more “normal”.

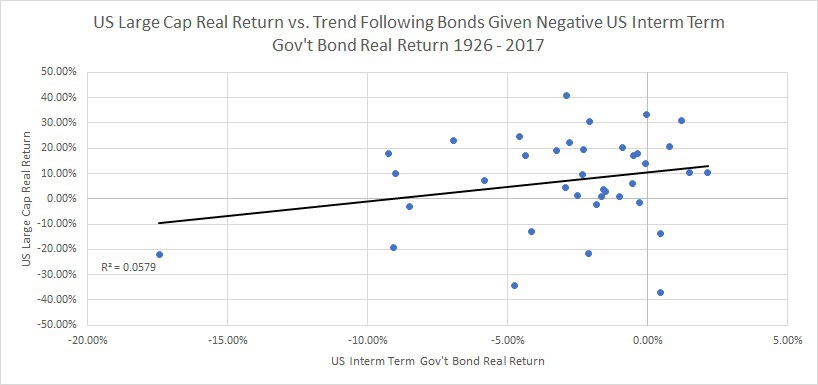
Negative bond return regime

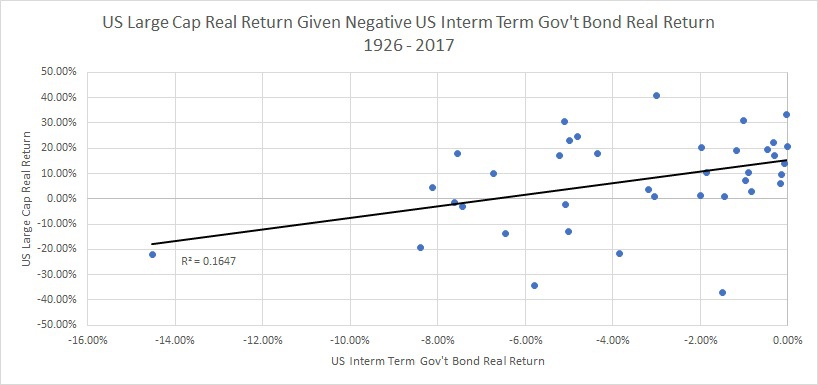
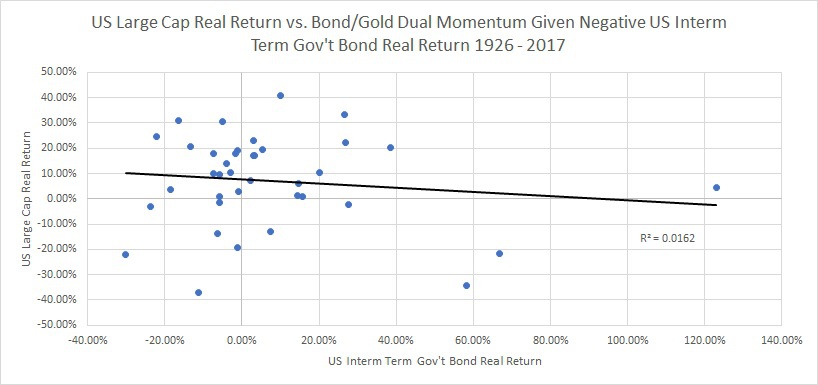
Below, I show the scatter plot for correlation of stocks and bonds, given that bonds had a negative real return:

Surprisingly, this shows that if bonds experience negative real returns then stocks and bonds tended to have a POSITIVE 41% correlation!  What is going on?

Why are Stocks/Bonds Positively Correlated when Bond Real Returns are Negative?

My hypothesis is that bonds and stocks actually share a common risk factor that negatively affects them both: inflation. Or more accurately — unexpected inflation. To test this hypothesis I use total return data from Ibbotson, data from the Consumer Price Index All-Urban Consumers Seasonally Adjusted (CPI) for inflation, and data from the Livingston Survey for expected inflation (starts in 1970). I break the actual CPI into two components 1) expected inflation (from the Livingston Survey) and 2) unexpected inflation (realized CPI – expected inflation). We can now run a regression on stocks and bond returns versus expected and unexpected inflation to see how stock and bond returns are affected by those two series.

I summarize the results, below:

The regression analysis suggests that both stocks and bonds respond negatively to unexpected inflation (if inflation is lower than expected it has helped boost the returns of stocks and bonds and if is higher than expected it hurts both of their returns). Given that, historically, inflation has tended to surprise far more to the upside (since 1970 unexpected inflation has averaged 0.6% per year) this likely drives the correlation of stocks and bonds when bond real returns are negative.

What is the Impact of Higher Correlations Between Stocks and Bonds?

Does assuming a conditionally higher correlation between stocks and bonds even matter? How big of a difference can it make in portfolio volatility? Let’s take a look at three scenarios for a 50% stock and 50% bond portfolio informed by history.

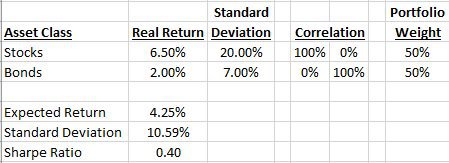
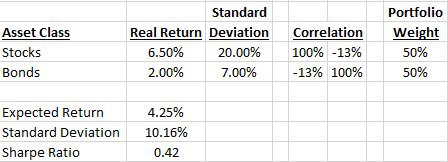
The first scenario we will analyze is a “standard” set of assumptions where the correlation between stocks and bonds is assumed to be zero:

This scenario will serve as a baseline portfolio to compare the other portfolios. We see that the standard deviation of the portfolio is assumed to be 10.6% per year and the Sharpe ratio is 0.40.

The second scenario we will analyze is the same portfolio, but this time we will assume that the real return on bonds is positive and therefore the correlation between stocks and bonds is -13%:

What we see here is that changing the correlation assumption decreases the standard deviation from 10.6% to 10.16% per year and increases the Sharpe ratio 5% to 0.42. In reality, these aren’t very big changes. Therefore, if we were to know that bonds were going to have a positive real return, it likely wouldn’t change portfolio construction very much.

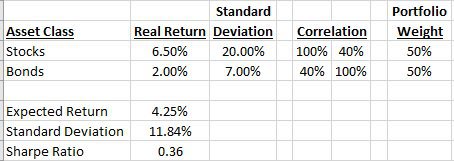
The final scenario we will analyze is that assuming bond real returns are negative and therefore stock and bonds return have a positive 40% correlation:

What we see now is that the standard deviation of the portfolio increases from 10.6% per year to 11.8% per year and the Sharpe ratio declines from 0.40 to 0.36. This has a meaningful impact on the portfolio and therefore would have implications for portfolio construction.

Great, Thanks for the Update — But What’s the Solution?

The analysis above highlights that bond allocations can be valuable for a portfolio, but it is regime dependent. To the extent there is positive unexpected inflation on the horizon, bonds might be a bad diversifier. In this section we examine several potential solutions to add diversification to a portfolio when it is needed most (when inflation surprises to the upside). First, one could trend follow their bond portfolio and shift between bonds and cash. The second solution is to add an inflation-friendly asset class like commodities.

Let’s examine each solution.

Trend Follow Bonds?

Trend following is a form of momentum investing that owns asset classes that are appreciating and doesn’t own asset classes (or even goes short) when they are declining. For more on the topic, check out this post by Wes. Trend following is generally thought of as a risk management technique and not normally a method to enhance returns, Corey Hoffstein has a great article here, that explains why trend following isn’t traditionally an offensive tool but a defensive one.

To examine if trend following bonds can help increase the diversification benefits, I create a trend follow bond return series. I create this series by assuming that if the current interest rate is less than its 12-month moving average then it owns the Ibbotson Intermediate-Term Government Bonds for the next month, if it is above its 12-month moving average then the portfolio owns cash. So does adding this level of risk management improve the correlation profile?

I show the resulting graphs, below:

What we see from the graphs is that adding trend following to bonds does enhance portfolio diversification potential. For example, when long only bonds have a positive real return (top graph), the correlation is -8% (vs. -13% for long only bonds) and when long only bonds had a negative real return (bottom graph), the correlation declined to 24% (versus 41% for long only bonds).

Adding a trend following risk management system to bonds did lower/flatten the correlation between regimes as unexpected inflation still hurts and investor that owns cash. Perhaps a stronger inflation hedge is necessary to help diversify a portfolio.

Relative Strength on Bonds and Commodities?

Perhaps the best way to hedge positive unexpected inflation (notice I am not saying inflation in a general sense), is to own commodities. There are lots of potential issues to consider when investing in commodities (see this excellent and massive post from Wes here). In addition to investment considerations, the history on commodities is sparse and sometimes not relevant as many commodities had fixed prices when the United States was on the gold standard. To try and work around this issue, I am going to make the following assumptions 1) I am going to focus on a single commodity – gold 2) I use a “Frankenstein” data series that uses gold miners during the US Dollar gold standard and physical gold after (to see why commodity companies may be a noisy proxy for the physical commodities, please see this post by Wes) and 3) I am ignoring contango and/or storage and insurance costs for physical gold as I am not as worried about the magnitude of returns as I am with the correlation structure of the returns.

Because of some of the issues with commodities, an investor may not want to own commodities all of the time, therefore I use one leg of the dual momentum concept (please see Gary Antonacci’s book and website for a more in-depth look at dual momentum) where either bonds or gold are owned based on which asset has the best performance over the prior 12 months. Let’s take a look at the results to see if dual momentum on bonds and commodities helps increase the diversification of portfolios irrespective of inflation regime.⁽¹⁾

Below are the graphs:

The results are exactly what we would want to see from a diversification standpoint – when the real return on bonds are negative (i.e., positive unexpected inflation), a bond/gold dual momentum portfolio has a -13% correlation with stocks (versus +24% with trend following bonds and 41% with long-only bonds) and when the real return on bonds are positive (i.e., “normal” times), a bond/gold dual momentum portfolio has a +27% correlation to stocks (versus -8% for trend following bonds and -13% for long only bonds).

This type of portfolio is interesting from a correlation perspective but could be difficult to add to a portfolio due to the volatility of gold and also being binary in picking regimes between bonds and gold. In reality, one would want to blend or dilute a gold/bond dual momentum portfolio to keep risk levels consistent and not take any unintended risks with a portfolio.

Conclusions

Hopefully, this post has highlighted that making simple assumptions (even informed by historical data) can mask interesting and important relationships between asset class returns. We see that the correlation between stocks and bonds is regime dependent and can vary greatly depending on if bond real returns are positive or negative and this relationship is likely driven by a common risk factor between stocks and bonds – their sensitivity to unexpected inflation.  Although interesting in theory, this revelation has important implications for portfolio construction as changing the correlation assumptions between stocks and bonds can materially increase the standard deviation of a portfolio and lower the Sharpe ratio.

What look at ways to keep portfolios diversified even when real bond returns are negative (positive unexpected inflation) and note that trend following bonds can help but doesn’t go far enough. We see that adding a dual momentum portfolio of gold/bonds does provide the type of diversification that an investor would look for if/when unexpected inflation shows up and hurts both stock and bond returns.