We at ENJINE are big believers in the potential of machine learning (or as some call, “artificial intelligence”) to transform asset management. However, it’s fair to say that machine learning hasn’t received mass adoption in the industry – yet. There are some great primers to get you going on the blog notably Druce Vertes post titled: “Machine Learning for Investors: A Primer” and a search will turn up many more. Our goal in this post though is to run through an example and develop a framework of how AI is utilized letting you see how the sausage is made.
There are a few reasons why machine learning hasn’t caught on, but one of the primary reasons is due to confusion around how to use it. The consensus opinion is that computer scientists can just feed raw data into a machine learning algorithm, and like a magician pulling a rabbit out of a hat, the algorithm makes sense of the data and spits out useful results.
Unfortunately, making sense of raw data requires intuitive reasoning, and machine learning algorithms don’t yet have that ability. Algorithms, therefore, need heavy guidance, but once they’re properly guided, they have an amazing ability to derive insights from data in ways that humans typically do not. What does this guiding look like? To answer that question, I’ll walk you through a simplified example of how we at ENJINE design machine learning models. Specifically, I’ll design a model that attempts to predict factor performances using past performance data.
Factor Timing Hypothesis
We can think of plausible reasons why past factor performance would influence future performance. Since we safely reside in fantasy land, let’s assume the value factor has had a good run recently (my sincerest condolences to Wes :-)). In this scenario, funds that employ the value strategy would see their AUMs increase due to the combination of performance gains and an influx of new investors. The same funds would then invest more money into value stocks, lifting the price of those stocks further. Of course, we can think of the opposite scenario happening where poor factor performance leads to continued poor results [cough][cough]value[/cough].
Using this intuition, we formulate our hypothesis such that there’s a sentiment state that affects whether factors will perform well in the future, and that past factor performances influence these sentiments. We then design a machine learning algorithm that reflects this hypothesis.(1)
One obvious way to represent sentiment is to use a numerical variable. A positive number indicates positive sentiment and vice versa. The sentiment’s evolution will depend on two sources of data – past sentiment (because sentiment changes gradually), and recent performance. We can mathematically express this belief as follows:
new sentiment = [(sentiment retention variable) x (past sentiment)] + [(new performance influence variable) x (new performance)]
After we iteratively update the sentiment with past performance data, we can then attempt to predict future factor performances using the following formula.
expected factor performance = (sentiment scaling variable) x (final sentiment)
Now that we’ve set up the structure of the algorithm, our goal now is to find the best values for sentiment retention variable, new performance influence variable, and sentiment scaling variable such that the expected factor performance aligns most closely to actual performance.
How do we do that?
This is where the magic of machine learning comes into play. We train machine learning algorithms by feeding the model with historical data. For example, data may indicate that momentum factor performances were -0.6%, +1.0%, …, +0.2% from May 2015 to Apr 2018, and that that the 3-month performance of the factor was +2.1% from May 2018 to Jul 2018. The machine learning model first tries some random numbers for the variables, calculates the expected factor performances using past performance data (i.e. May 2015 to Apr 2018 data), and then determines which variable numbers appeared to have predicted future performance (i.e. May 2018 to Jul 2018 data) best. It would then make intelligent guesses to find better variable numbers that improve the predictions.
Bayesian Approach and Priors
There are two major approaches to finding the best variable numbers – Frequentist and Bayesian. The Frequentist approach is more common, and it treats each of the variables as single point numbers, not statistical distributions. In other words, it may assign a single value of ‘0.52’ to the sentiment retention variable, as opposed to a range between ‘0.3 to 0.7’. While the Frequentist approach is simpler, it’s more prone to overfitting (i.e. learning bad lessons from data), particularly when working with small and/or noisy data sets.
The Bayesian approach, on the other hand, models each variable as statistical distributions.(2) In other words, it acknowledges that there’s some uncertainty in what the variable numbers should be. In addition to being more resistant to overfitting, the Bayesian approach allows us to incorporate some ‘prior’ beliefs about the variables to help the machine learning model train better. As we’re dealing with a small noisy data set, the Bayesian approach is favored for its flexibility.
In order to use the Bayesian approach, we need to set priors for each variable. Let me explain how I set them.
- sentiment retention: This variable determines how much of the past sentiment carries over into the next month. I thought it would be reasonable to expect that the magnitude of the sentiment carried over will decrease over time. Memories tend to fade, not amplify. This led me to constrain the absolute value of the variable to less than or equal to 1.
The good news regarding “priors” is that we can play defensive – if we’re not sure whether a variable can take on a set of values, we can always elect to allow for the possibility in the prior and let the data decide if those values make sense. For example, my assumption is that sentiment won’t flip from positive to negative each month, but I wasn’t sure. Therefore, to be defensive, I allowed for the possibility of sentiment to flip. To express the belief that sentiment retention can take on any value from -1 to 1 with equal probability, I set the prior statistical distribution to be the uniform distribution from -1 to 1.
- new performance influence: I wasn’t sure what the effect of recent performances would be on the sentiment, but I didn’t believe that the magnitude of the effect would be extremely large. For example, I didn’t think a +2% monthly performance would have 10 times (i.e. +20%) magnitude effect on sentiment. To express this belief, I chose to use a normal distribution with 0 mean and 5 standard deviation for the prior, which only allows for a 5% chance that the magnitude of the new performance influence is greater than 10.
- sentiment scaling: We’re trying to forecast the future quarterly return, and I believed that the sentiment state should have a comparable magnitude to that of monthly returns, so a rough guess of 3 made sense as the variable’s value. I thought the variable is more likely to be positive than negative, but I wanted to allow for the possibility that the value is negative. I also wanted to allow for a wide range of values to be possible (since 3 is just a very rough guess), so I chose the prior to be a normal distribution with a mean of 3 and a standard deviation of 10.
- model uncertainty: We didn’t discuss this variable before, but it’s necessary for the Bayesian approach. Our model not only tries to predict the future factor performances, but it also tries to model the uncertainty around the predictions as well by finding the correct standard deviation around the prediction. I thought it reasonable to assume that model uncertainty would be of similar magnitude to quarterly returns, which is roughly 8%. Standard deviation values must be positive, and since I assumed that values above 20% is unlikely, I’ve used the half Cauchy distribution with median value of 20% as the prior for the model uncertainty.
Results
With the structure of our algorithm and our priors defined, I then wrote the code that trains our model. In order to gauge the efficacy of the model, I first split the data into the training and test data sets. I trained only using the training data, and made predictions only using the test data set. I periodically plotted the predictions vs. actual factor performances. You can view and run my code HERE. I recommend running each cell from beginning to end, in order.
When you train the first data set, you’ll notice a few things. First, you’ll notice that the y-axis (predictions) range shrinks with more iterations. The machine learning model initially tries to make bold predictions (high magnitude predictions), but becomes more timid (i.e. makes predictions close to 0) as it finds it can’t make good predictions.
You’ll notice that the code prints out something called ‘ELBO’. This is a measure of how well the current model fits the data. All you need to know about these values is that lower numbers indicate better fits. You can ignore the number otherwise.
Finally, you’ll notice the R2 (R-squared) number is generally negative. Some of you might wonder how R2 can be negative if it’s the square of the correlation coefficient. However, that definition of R2 is only one of several, and using that definition can potentially overstate the predictive capability of a model by rewarding spurious correlations. Instead, we use a stricter definition of R2, such that a positive value would more confidently indicate predictive capabilities.
When training is complete, you’ll notice that the final model generally has R2 hovering near 0, indicating that the model has no predictive capabilities. You’ll also sense the same by looking at the graphs produced. I’ve tried tweaking the model several different ways, but still wasn’t able to produce R2 values above 0.
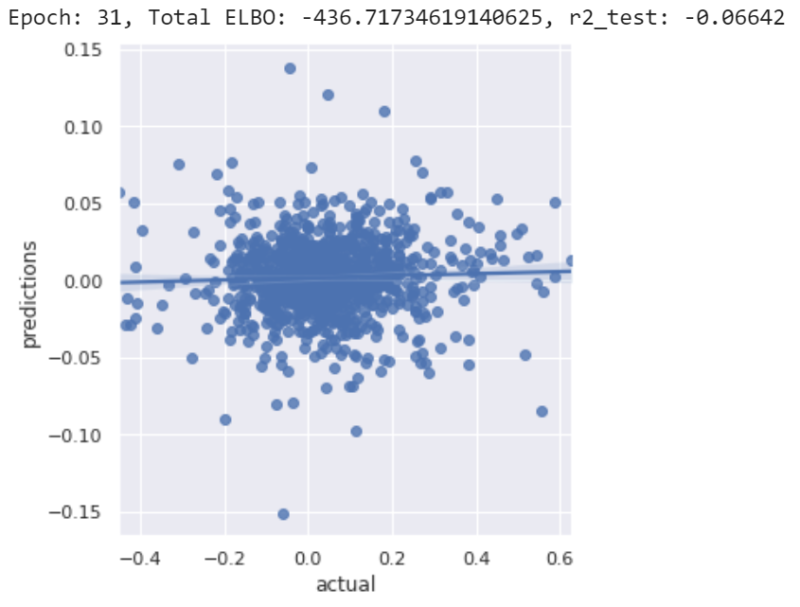
So what can we conclude from our experiment? It means the model structure we developed can’t predict future factor performance. Don’t trick yourself into thinking that our results mean we can never predict future performance using past performance. Rather we need to develop and test new models and hypotheses combined with new data sets that might include macroeconomic, technical, or other miscellaneous sources of information.
Summary
Although our experiment wasn’t able to show you a useful result using machine learning, I hope you now have some insight into how machine learning models are designed. Far from being black boxes whose switch you just need to turn on, machine learning models require careful thought and consideration. Luckily, the mental efforts we spend are often rewarded with tangible results, and that’s why we as a firm are very excited about the potential of machine learning ahead.
References[+]
| ↑1 | Related to reflexivity |
|---|---|
| ↑2 | See here for an application of bayesian methodologies in finance. |
About the Author: Jin Won Choi
—
Important Disclosures
For informational and educational purposes only and should not be construed as specific investment, accounting, legal, or tax advice. Certain information is deemed to be reliable, but its accuracy and completeness cannot be guaranteed. Third party information may become outdated or otherwise superseded without notice. Neither the Securities and Exchange Commission (SEC) nor any other federal or state agency has approved, determined the accuracy, or confirmed the adequacy of this article.
The views and opinions expressed herein are those of the author and do not necessarily reflect the views of Alpha Architect, its affiliates or its employees. Our full disclosures are available here. Definitions of common statistics used in our analysis are available here (towards the bottom).
Join thousands of other readers and subscribe to our blog.

