When stock prices reach a new high, investors start asking the question:
Are stocks overvalued?
To answer this question, investors have developed several alternative equity valuation models. Typically, each of these models compares the stock market’s current price level to a benchmark. Among practitioners, two of the leading equity valuation models are the Shiller CAPE model and the so-called Fed model. Thought leaders in the space debate the merits of the different approaches. For example, at the 70th Annual CFA Institute Conference in 2017, there was a heated debate between Robert Shiller and Jeremy Siegel on whether the US stock market is overvalued(1). On the one hand, Robert Shiller, the distinguished Yale economist and Nobel Laureate, claimed that the US stock market is highly overvalued judging by the current CAPE ratio. On the other hand, Jeremy Siegel, the author of “Stocks for the Long Run”, remarked that, given the extremely low-interest rates, the US stock market is not overvalued. Janet Yellen, the previous Fed Chair, held the same opinion as Jeremy Siegel. In particular, at the end of 2017, she said that “the low-rate environment is supportive of higher CAPE ratio.” Apparently, both Jeremy Siegel and Janet Yellen use the Fed model to determine whether the US stock market is overvalued.
In this piece, we’ll dig into the two leading models and examine the empirical evidence on both approaches. We come to the following conclusions:
- The Fed model was valid during the period from 1958 to 2010. Since after 2010 there has been no relationship between the stock’s earnings yield and the bond yield, the Fed model cannot be used to judge whether the US stock market is overvalued. In other words, the Fed model cannot support the high current CAPE ratio on the grounds of the low-rate environment. Thus, both Jeremy Siegel and Janet Yellen might be wrong about the current state of the market.
- The Shiller model is arguably over-simplistic. It is justified only on the grounds that there is an empirical inverse relationship between the CAPE value and the subsequent stock market return over horizons ranging from 10 to 15 years. What is less known about the validity of the Shiller model is that it has forecasting power only for real returns. For nominal returns, the validity of the Shiller model is much less convincing.
- The other serious problem with the Shiller model is that it cannot be successfully used to time the market. The difficulties with using the Shiller model to time the market are described in Asness, Ilmanen and Maloney (2017) and further discussed in this article.(2)
- We don’t have a silver bullet model that solves all the problems with the current models available, however, in a more detailed paper available here, we explore this topic in more detail.
Note. The Alpha Architect deep dive on building out expected return forecast models is here.
Shiller CAPE Model
CAPE stands for the “Cyclically Adjusted Price-to-Earnings ratio”. It is the ratio of the price of the S&P 500 index to the 10-year moving average of earnings. The Shiller CAPE model was introduced by Campbell and Shiller (1998) and further popularized and developed by Shiller (2005).(3)(4) The Shiller model is based on a simple mean reversion theory that states that when stock prices are high relative to recent earnings, then prices will eventually fall in the future to return the price-to-earnings ratio to a more normal historical level. Using this model, Campbell and Shiller (1998) predicted the stock market crash of 2000 on the basis of an unreasonably high CAPE ratio. Since that time, the Shiller model has been extremely popular among practitioners.
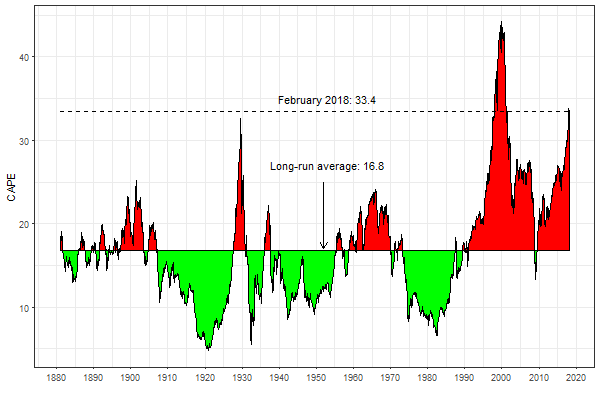
The figure below plots the Shiller CAPE ratio. The solid horizontal line shows the location of its long-run average. The long-run mean value of the CAPE amounts to 16.8. Whether the stock market is overvalued or not is gauged by comparing the current value of the CAPE ratio with its long-run mean. Therefore, the shaded green (red) areas highlight the periods where the stock market was undervalued (overvalued). The current (as of February 2018) CAPE ratio is 33.4. That is, the current CAPE ratio is double as much as its long-run average. This fact suggests that the US stock market is highly overvalued. The dashed horizontal line shows the location of the current CAPE. Apparently, the current degree of the stock market overvaluation exceeds that which was observed near the Great Crash in October 1929. As a matter of fact, judging by the CAPE model, the stock market in the US has been overvalued over the course of the last (almost) 30 years.
-
The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index.
Fed Model
The Fed model postulates that the stock’s earnings yield should be approximately equal to the long-term bond yield. Formally, the Fed model postulates the following:
E/P = Y or, CAPE= 1/Y,
where E/P is the stock market earnings-to-price ratio and Y is the yield on the long-term (government) bonds. The idea is that investors can invest either in stocks or long-term bonds and, therefore, stocks and bonds are two major competing assets. If, for example, the bond yield increases, stock prices should decrease in order for the stock’s earnings yield to increase to maintain the competitiveness of stocks. Empirical support for this model is found in many academic studies.
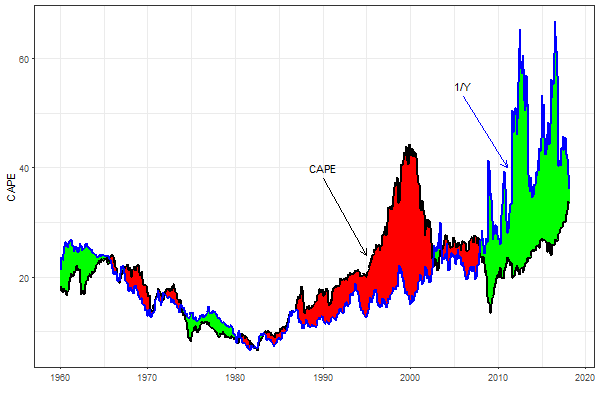
The figure below plots the Shiller CAPE ratio (black line) versus 1/Y (blue line). Whether the stock market is overvalued or not is gauged by comparing the current value of the CAPE ratio with the value of 1/Y. As before, the shaded green (red) areas highlight the periods where the stock market was undervalued (overvalued). The Fed model suggests that the stock market was severely overvalued during the second half of the 1990s, but the Dot-Com bubble crash corrected the market prices to their normal values.
According to the Fed model, the US stock market has been severely undervalued beginning from 2009. Yet, the current degree of the US stock market overvaluation is very moderate.
-
The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index.
However, the Fed model has often been criticized on theoretical and empirical grounds. From the theoretical point of view, the Fed model can be reconciled with the existing financial theory under very restrictive assumptions. On empirical grounds, the Fed model is shaky: Several academic studies report that the Fed model is supported by data that starts from around 1960, however, prior to this date, there is no empirical support for the Fed model.
Graham Model
Even though the Fed model lacks a solid theoretical underpinning, the majority of academics and practitioners agree that there should be a relationship between the stock’s earnings and bond yields. The Fed model is very restrictive and was first mentioned for the US in a July 1997 Federal Reserve Monetary Policy Report to Congress by Alan Greenspan. Long before Alan Greenspan’s mentioning of the Fed model, Benjamin Graham, a legendary investor and the father of value investing, advocated for a much less restrictive relationship between the stock’s earnings and bond yields.
Graham’s central idea was that the value of a stock usually differs from its price. Therefore, the stocks should be bought (sold) when the market is undervalued (overvalued). To identify whether the stock market is overvalued or not, Graham developed an approach which was inspired by the methodology previously employed by Roger Babson (see Graham and Dodd, 1934, Chapter 50).(5)
First of all, Graham claimed that under “normal” market conditions, the relationship between the stock earnings yield and the bond yield must be,
E/P=M*Y,
where M denotes a suitable “multiplier”. Graham suggested that, “The multiplier might be equivalent to capitalizing the earnings at, say, twice the current interest rate on highest grade industrial bonds.” However, since the value of the multiplier is determined ad-hoc, one should not buy (sell) stocks right after the current E/P ratio crosses from above (below) the value of M*Y. Graham’s second suggestion was that one should purchase stocks only at a substantial discount from the normal value. Specifically, Graham advocated for buying stocks when the current E/P ratio is at 80% of normal value. Similarly, selling stocks is sensible when the current E/P ratio is at 120% of normal value. Overall, the Graham model can be interpreted as follows. The market is more or less fairly priced when,
0.8*M*Y < E/P < 1.2*M*Y.
That is, when the current E/P ratio lies within 20% band around M*Y.
In a recent working paper, Zakamulin and Hunnes (2018) examine the empirical validity of the Graham model using US data that spans a very long historical period, 1871 – 2016.(6) The working hypothesis in this paper is that there is an equilibrium relationship between the stock’s earnings and bond yields, but this equilibrium relationship is subject to evolutionary changes. Using the modern methodology of detecting multiple breakpoints, the authors find the structural breaks in the relationship between the stock’s earnings and bond yields, investigate the direction of causality in the relationship, and try to explain the causes of the breaks. The results of this study shed new light on how the investors have evaluated stocks relative to bonds. These results also contribute to the ongoing debate on whether the US stock market is overvalued or not.
Empirical Support for the Graham Model
The empirical results reported by Zakamulin and Hunnes (2018) can be summarized as follows:
- The structural break analysis identifies two major breaks in the relationship between the stock’s earnings and bond yields: in 1929 and in 1958.
- Moreover, the co-integration analysis advocates for the presence of the equilibrium relationship between the two yields over the periods 1871-1929 and 1958-2016. In other words, the relationship broke down in 1929 and was later re-established in 1958. Perhaps the most important and surprising finding of this empirical study is that the multiplier in the relationship E/P = M*Y has changed from M=2 over the period from 1871 to 1929 to M=1 over the period from 1958 to 2016.
- Last but not least, there are clear indications that a new break in the relationship occurred around 2010.
Zakamulin and Hunnes (2018) try to provide answers to the following two major questions:
Why there was no relationship between the stock’s earnings yield and the bond yield over the period from 1929 to 1958?
and,
Why the multiplier in the equilibrium relationship has changed from M=2 to M=1?
In brief, the story goes as follows. The breakdown of the equilibrium relationship in 1929 is explained by the stock market crash and the following depression forcing the Fed to start conducting an expansionary monetary policy by lowering the short-term interest rate to nearly zero and decreasing substantially the long-term interest rate. Due to the government needs to finance the World War II and subsequent recession that ended in 1949, the interest rates were deregulated only in the early 1950s. The main argument for the re-establishment of a completely new equilibrium relationship between the two yields is that a major “paradigm shift” in the stock valuation theory occurred in the late 1950s. To combat the Global Financial Crisis of 2007-08, from about 2009 the Fed lowered the short-term interest rate (a.k.a. the federal funds rate) to virtually zero. This explains the new recent break in the equilibrium relationship that occurred in 2010.
The study by Zakamulin and Hunnes (2018) also provides an important insight into the causality relationship between the stock’s earnings yield and the bond yield. Specifically, the econometric methodology allowed the authors to find out which of the two yields is the cause of the change in the value of the other yield in the relationship. This analysis reveals that in both historical segments 1871-1929 and 1958-2010, the stock’s earnings yield followed the bond yield in both the short-run and the long-run, but not the other way around. Put differently, the analysis clearly indicates that the Fed monetary policy influences the stock prices. For example, by lowering the bond yield the Fed is able to boost the stock prices. However, this is only possible under the “normal” market conditions when the investors believe in the existence of the relationship E/P = M*Y. During the periods where the Fed lowers the short-term interest rate to nearly zero, the relationship breaks down and, as a consequence, the stock’s earnings yield decouples from the bond yield.
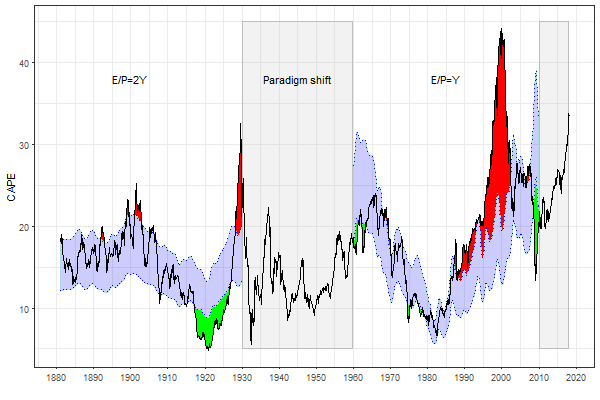
The working of the Graham models is illustrated in the figure below that plots the Shiller CAPE ratio. The blue shaded areas highlight the two periods (1881-1929 and 1958-2010) where the empirical analysis identifies the presence of the equilibrium relationship between the stock’s earnings yield and the bond yield. Each blue shaded area represents the 20% band around the “normal” relationship between the two yields. The stock market is overvalued (undervalued) when the current CAPE ratio lies above (below) the blue shaded area. As before, the shaded green (red) areas highlight the periods where the stock market was undervalued (overvalued). The gray shaded areas highlight the two periods (1930-1957 and 2010-now) without the equilibrium relationship between the two yields.
-
The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index.
According to both the Shiller and Fed models, the stock market is constantly in disequilibrium. In contrast, according to the Graham model, the stock market is most often in the equilibrium when there is a long-run relationship between the two yields. For example, the Shiller model advocates that from the late 1950s to the early 1970s the stock market was overpriced, whereas from the early 1970s to the late 1980s the stock market was underpriced. The Graham model, on the other hand, says that from the late 1950s to the late 1980s the stock market was more or less fairly priced. The stock market was severely overpriced during the second half of the 1990s, but the Dot-Com bubble crash corrected the market prices to their normal values. The Graham model suggests that the stock market was more or less fairly priced from 2003 to 2008. Only during 2008 was the stock market substantially undervalued.
Concluding Remarks
First of all, note that the Fed model is a particular case of the more general Graham model. The results by Zakamulin and Hunnes (2018) suggest that the Fed model was valid during the period from 1958 to 2010. Since after 2010 there has been no relationship between the stock’s earnings yield and the bond yield, the Fed model cannot be used to judge whether the US stock market is overvalued. In other words, the Fed model cannot support the high current CAPE ratio on the grounds of the low-rate environment. Thus, both Jeremy Siegel and Janet Yellen could be wrong about the current state of the market.
The fact that both Jeremy Siegel and Janet Yellen seem to be wrong does not necessarily mean that Shiller is “right,” and the market is highly overpriced. The Shiller model is over-simplistic. It is justified only on the grounds that there is an empirical inverse relationship between the CAPE value and the subsequent stock market return over horizons ranging from 10 to 15 years. What is less known about the validity of the Shiller model is that it has forecasting power only for real returns. That is, for the returns adjusted for inflation. For nominal returns, the validity of the Shiller model is much less convincing.
The other serious problem with the Shiller model is that it cannot be successfully used to time the market. The difficulties with using the Shiller model to time the market are described in Asness, Ilmanen and Maloney (2017).(7) Two simple illustrating examples are as follows. If the investor believes in the validity of the Shiller model, this investor should buy the stocks in the early 1970s. However, in this case, the investor would be highly disappointed because the stock prices had been decreasing till the early 1980s. Similarly, if the investor uses the Shiller model, this investor would sell stocks in the early 1990s, missing out on huge net gains over the full bull/bear cycle.(8)
The main difficulty in using the Shiller model for timing the market is the following. Recall that the Shiller model is based on the mean-reversion idea. However, mean reversion is an ambiguous concept and exists in several different forms. In the Shiller model, the concept of mean reversion can be expressed by the common investment wisdom that “over time, markets tend to return to the mean”. For example, when the CAPE moves far in one direction, this movement will eventually be reversed, and the CAPE returns back to its mean. However, mean reversion in the CAPE is much more than simply returning to the mean. In reality, the movement is far greater. This type of mean reversion incorporates further common investment wisdom, namely, that “an excess in one direction will lead to an excess in the opposite direction.” That is, when the CAPE moves too far in one direction, it will not merely return to the mean but overshoots in the opposite direction. For example, a period of above-average CAPE tends to be followed by a period of below-average CAPE and vice versa. The problem is that the cyclical fluctuations in the CAPE are of irregular nature and, therefore, one cannot predict the turning points in the CAPE dynamic.
Acknowledgments
The author is grateful to Arngrim Hunnes and Fred J. Penney for their valuable comments.
References[+]
| ↑1 | Prof. Siegel will be at Democratize Quant next week! |
|---|---|
| ↑2 | recapped and discussed here as well. |
| ↑3 | Campbell, J. Y. and Shiller, R. J. (1998). “Valuation Ratios and the Long-Run Stock Market Outlook”, Journal of Portfolio Management, 24 (4), 11–26. |
| ↑4 | Shiller, R. J. (2005). Irrational Exuberance. 2nd edition, Princeton University Press. |
| ↑5 | Graham, B. and Dodd, D. (1934). Security Analysis. Whittlesey House, New York. |
| ↑6 | Zakamulin, V. and Hunnes, A. (2018). “Stock Earnings and Bond Yields in the US 1871 – 2016: The Story of a Changing Relationship”. Working paper, University of Agder, Norway, available at SSRN |
| ↑7 | Asness, C., Ilmanen, A., and Maloney, T. (2017). “Market Timing: Sin a Little”, Journal of Investment Management, 12 (1), 27–63. |
| ↑8 | This post has information on the various CAPE-based approaches |
About the Author: Valeriy Zakamulin
—
Important Disclosures
For informational and educational purposes only and should not be construed as specific investment, accounting, legal, or tax advice. Certain information is deemed to be reliable, but its accuracy and completeness cannot be guaranteed. Third party information may become outdated or otherwise superseded without notice. Neither the Securities and Exchange Commission (SEC) nor any other federal or state agency has approved, determined the accuracy, or confirmed the adequacy of this article.
The views and opinions expressed herein are those of the author and do not necessarily reflect the views of Alpha Architect, its affiliates or its employees. Our full disclosures are available here. Definitions of common statistics used in our analysis are available here (towards the bottom).
Join thousands of other readers and subscribe to our blog.