Time Series Momentum in the US Stock Market: Empirical Evidence and Theoretical Implications
- Valeriy Zakamulin and Javier Giner
- Working paper, University of Agder and University of La Laguna
- A version of this paper can be found here
What are the Motivations?
The profitability of trend-following strategies has been documented in a large number of empirical studies. The majority of these empirical studies find that these strategies are profitable in the long-run over periods ranging from 50 to 150 years. However, two issues of concern arise regarding the empirical performance of trend-following strategies. The first issue is that the researchers frequently report that, when they use the most recent 5 to 10 years in their sample of historical data, the trend-following strategies are not profitable. This issue may imply that market efficiency improves over time and the trend-following strategies are no longer profitable. Another issue is the lack of scientific evidence on the profitability of trend-following strategies. Specifically, even when the historical sample is rather long and the profitability of trend-following strategies is highly economically significant, quite often the researchers cannot reject the null hypothesis that the performance of a trend-following strategy is similar to the performance of the corresponding buy-and-hold strategy. In short, is trend-following a genuine economic phenomenon or a data-mining exercise?
Time-series momentum strategy (TSMOM, also referred to as “absolute momentum” by practitioners) presented by Moskowitz et al (2012), is an example of a trend-following strategy. Using a comprehensive dataset of different asset classes, Moskowitz et al (2012) demonstrate that the past 12-month returns predict the next month return; a trading strategy, which buys assets if their past 12-month returns are positive and sells these assets otherwise, earns significant risk-adjusted returns. However, the results reported by Moskowitz et al (2012) have been heavily criticized. Specifically, Kim et al (2016) find that the results by Moskowitz et al (2012) are largely driven by volatility-scaling returns rather than by short-term momentum effect.(1) Huang et al (2020) show, among other things, that asset-by-asset time series regressions reveal almost no evidence of short-term momentum. For example, they find no evidence of short-term momentum in the S&P 500 index. Even a pooled regression does not provide evidence of momentum. All in all, the papers by Kim et al (2016) and Huang et al (2020) cast serious doubts on the existence of short-term momentum in financial markets.
What are the Research Questions?
Academic literature highlights the controversy regarding the profitability of trend-following strategies and the existence of short-term momentum.
The core questions under investigation are as follows:
- Are there short-term trends in financial markets?
- What is the type of process that generates these trends?
- Are trend-following strategies profitable? If so, why are the results so controversial?
What are the Findings?
First of all, based on the results of an empirical study, this paper presents compelling evidence of short-term momentum in the US stock market.
It is further assumed that the excess returns follow an autoregressive process of order p, AR(p), and the parameters of this process are estimated. The difficulty is that over monthly horizons the autocorrelation in excess returns is very weak and escapes detection when traditional estimation methods are used. A novel methodology is suggested that uses excess returns aggregated over multiple months and finds the parameters of the AR(p) process that produce the best fit to a theoretical model. The parameters of the AR(p) process are evaluated under the simplifying assumption that the TSMOM rule with n return lags represents the most optimal trading rule among all feasible trend-following rules.
In particular, this paper provides analytical results on the Sharpe ratios of the long-only and long-short TSMOM strategies. The estimated parameters of the model for the excess returns are utilized to evaluate the profitability of these strategies. The evaluation results suggest that the long-short TSMOM strategy is not profitable, whereas the long-only TSMOM strategy has a clear edge over the buy-and-hold strategy (see the table below). Specifically, the estimated Sharpe ratio of the long-only TSMOM strategy is about 30% higher than that of the buy-and-hold strategy.
| Buy and hold | Long-only TSMOM | Long-short TSMOM | |
| Mean return, % | 0.856 | 0.864 | 0.872 |
| Std. deviation, % | 5.024 | 3.930 | 5.022 |
| Sharpe ratio | 0.107 | 0.139 | 0.110 |
The theoretical monthly mean return, standard deviation, and the Sharpe ratio of the buy-and-hold strategy, the long-only TSMOM strategy, and the long-short TSMOM strategy. The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged and do not reflect management or trading fees, and one cannot invest directly in an index.
The multi-period properties of the TSMOM strategy are studied by means of carrying out extensive and careful computer simulations. The paper finds that the shape of the probability density of multi-period returns to the long-only TSMOM strategy resembles the shape of the density function of returns to a portfolio insurance strategy (see the figure below). Therefore, the risk profile of the long-only TSMOM strategy is totally different from that of the buy-and-hold strategy. For example, the simulation results suggest that, as compared to the buy-and-hold strategy, over a 5-year horizon the long-only TSMOM strategy has a very different loss profile. Consequently, the advantage of the long-only TSMOM strategy over the buy-and-hold strategy lies not only in the higher Sharpe ratio, but also in the potential downside protection.
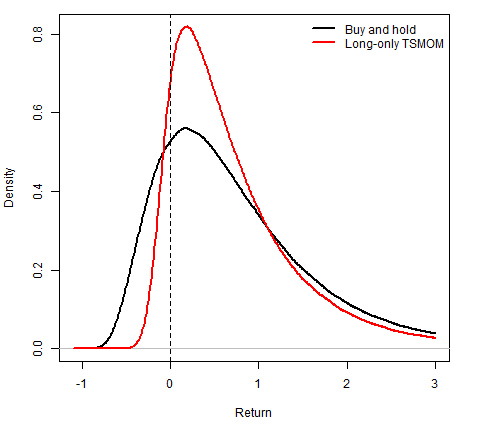
The results reported in the paper strongly suggest that over the long-run the long-only TSMOM strategy outperforms the buy-and-hold strategy on a risk-adjusted basis. But if this is the case, why is the existing evidence on trend-following controversial? The primary argument is that because of randomness and the fact that the trend strength is rather weak, over the short-run the outperformance of trend-following is shaky at best. We confirm this observation. Using a simulation analysis, the paper finds that over short- to medium-term horizons from 5 to 10 years, the probability that the TSMOM strategy outperforms the buy-and-hold strategy is less than 60%. Consequently, it is not surprising that in short samples the researchers often find that trend-following strategies are not profitable. By convention, the desired power of a statistical test is 80%. A ballpark estimate is that, in order to reach the desired power level, the sample size must be about 250 years with monthly observations. The clear-cut implication from this result is that any empirical study tends to not reject the null hypothesis of no profitability because the power of the statistical test is extremely low. (discussed here fairly recently)
Abstract
We start this paper by presenting compelling evidence of short-term momentum in the excess returns on the S&P Composite stock price index. For the first time ever, we assume that the excess returns follow an autoregressive process of order p, AR(p), and evaluate the parameters of this process. Armed with a fairly accurate knowledge of the momentum generating process, we continue this paper by providing a number of important theoretical implications. First, we present analytical results on the profitability of long-only and long-short time-series momentum (TSMOM) strategies. Our results suggest that the long-only TSMOM strategy is profitable, while the long-short one is not. We find that over multiple periods the risk profile of the long-only TSMOM strategy resembles the risk profile of a portfolio insurance strategy. We estimate the power of the statistical test for superiority of the TSMOM strategy and find that the power is much below the acceptable level. Consequently, any empirical study tends not to reject the null hypothesis of no profitability of TSMOM strategy. Finally, we evaluate the precision of identification of the optimal number of lags in the TSMOM rule using a standard back-testing methodology and find that this precision is extremely poor. However, we demonstrate that the performance of the TSMOM rule is robust to the choice of the number of lags.
References
- Moskowitz, Ooi, and Pedersen (2012), Time series momentum, Journal of Financial Economics, Volume 104, Issue 2, Pages 228-250
- Kim, Tse, and Wald (2016), Time series momentum and volatility scaling, Journal of Financial Markets, Volume 30, Pages 103-124
- Huang, Li, Wang, and Zhou (2020), Time series momentum: Is it there?, Journal of Financial Economics, Volume 135, Issue 3, Pages 774-794
About the Author: Valeriy Zakamulin
—
Important Disclosures
For informational and educational purposes only and should not be construed as specific investment, accounting, legal, or tax advice. Certain information is deemed to be reliable, but its accuracy and completeness cannot be guaranteed. Third party information may become outdated or otherwise superseded without notice. Neither the Securities and Exchange Commission (SEC) nor any other federal or state agency has approved, determined the accuracy, or confirmed the adequacy of this article.
The views and opinions expressed herein are those of the author and do not necessarily reflect the views of Alpha Architect, its affiliates or its employees. Our full disclosures are available here. Definitions of common statistics used in our analysis are available here (towards the bottom).
Join thousands of other readers and subscribe to our blog.

