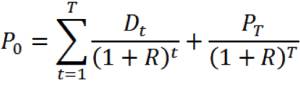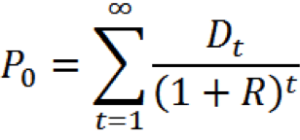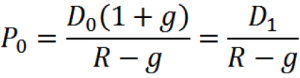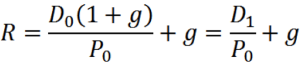Introduction to Finance: Class 4

Stock Valuation

What is stock valuation?

There are many ways to determine the value or worth of a stock (refamiliarize yourself with what a stock is).

Each stock is different, and each industry sector has unique properties that may require varying valuation approaches…Stock is sometimes referred to as shares, securities or equity.

—Source 

· · · · ·
Key Concepts:

• What is Common Stock?
• Common Stock Valuation
• Dividends
• Required Returns
• Current Value of a Stock

What is Common Stock?

• A share of stock represents an ownership stake in the firm

• More reading here

• An investor who buys a share of stock has two basic rights:

1. Control Rights
   • Voting right: elect representatives (directors) who hire management to run the firm
2. Cash Flow Rights
   • Right to share proportionally in dividends paid
   • Dividends are discretionary payments by corporation to shareholders in the form of cash or stock

• Equity Financing
  • Differences between Debt & Equity Financing (REVIEW)
    • Debt
      • Not an ownership interest
      • Creditors do not have voting rights
      • Interest is considered a cost of doing business and is tax deductible
      • Creditors have legal recourse if interest or principal payments are missed
      • Excess debt can lead to financial distress and bankruptcy
    • Equity
      • Ownership interest
      • Common stockholders vote for the board of directors and other issues
      • Dividends are not considered a cost of doing business and are not tax deductible
      • Dividends are not a liability of the firm, and stockholders have no legal recourse if dividends are not paid
      • An all equity firm can not go bankrupt merely due to debt since it has no debt

Common Stock Valuation

•  More difficult than bond valuation since:
  • Cash flows are not known
  • Stocks have an infinite life
  • Don’t know what rate of return market requires

• If you buy share of stock, you receive cash in two ways
  • The company pays dividends
  • You sell your shares either to another investor in the market or back to the company

• As with bonds, the price of the stock is the present value of these expected cash flows

One-Period Example

• Suppose you are thinking of purchasing the stock of Moore Oil, Inc.  You expect it to pay a $2 dividend in one year, and you believe that you can sell the stock for $14 at that time. If you require a return of 20% on investments of this risk, what is the maximum you would be willing to pay?
  • Compute the PV of the expected cash flows
  • Price = (14 + 2) / (1.2) = $13.33

Two-Period Example

• Now, what if you decide to hold the stock for two years? In addition to the $2 dividend in one year, you expect a dividend of $2.10 and a stock price of $14.70 both at the end of year 2. Now how much would you be willing to pay?
  • PV = 2 / (1.2) + (2.10 + 14.70) / (1.2)^2 = 13.33

Three-Period Example

• Finally, what if you decide to hold the stock for three periods? In addition to the dividends at the end of years 1 and 2, you expect to receive a dividend of $2.205 and a stock price of $15.435 both at the end of year 3. Now how much would you be willing to pay?
  • PV = 2 / 1.2 + 2.10 / (1.2)^2 + (2.205 + 15.435) / (1.2)^3 = 13.33

Developing the Stock Valuation Model

• You could continue to push back when you sell the stock

• You would find that the price of the stock is really just the present value:

• So, how can we estimate all future dividend payments?

Dividends

Estimating Dividends: Special Cases

• Constant dividend (zero growth)
  • The firm will pay a constant dividend forever

• Constant dividend growth
  • The firm will increase the dividend by a constant percent every period

• Supernormal growth
  • Dividend growth is not consistent initially, but settles down to constant growth eventually

Constant Dividend

•  If dividends are expected to be constant (Dt=D) at regular intervals forever, then value stock as a perpetuity
  • P0 = D / R
• Suppose stock is expected to pay a $0.50 dividend every quarter and the required return is 10% with quarterly compounding.  What is the price?
  • Quarterly required return = 10% / 4 = 2.5%
  • P0 = .50 / .025 = $20

Constant Dividend Growth Model

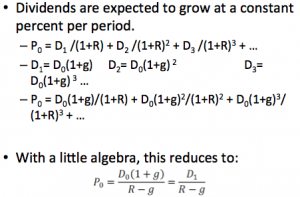
Dividend Growth Model: Example

• Suppose Joe’s Place, Inc. just paid a dividend of $.50. It is expected to increase its dividend by 2% per year. If the market requires a return of 15% on assets of this risk, how much should the stock be selling for?
  • P0 = D1 / (R – g)

• D1 = D0 x (1+g)
• D1 = 0.50 x (1+ 0.02) = 0.51

• P0 = 0.51 / (.15 – .02)
• P0= $3.92

Dividend Growth Model Assumptions

1. Stock grows at constant rate (g constant)
   • Product market the firm operates in “settles down” to a steady state
   • Firms manage dividend policy to foster constant growth

2. Required return exceeds growth rate (R > g)
   • Geometric series assumes “r” < 1 (or (1+g)/(1+R) < 1)
   • In long run, relation must hold
   • In short run, R may be less than g (supernormal growth problem)

Nonconstant Dividend Growth

• In short run, supernormal growth rate may exceed required return (g > R)
• In long run, dividend policy reverts to:

1. No future dividends
2. All future dividends are constant
3. All future dividends grow at a constant rate

Nonconstant Dividend Growth: Example

• Suppose a firm expects to increase dividends by 20% in one year and by 15% in two years.  After that, dividends will increase at a rate of 5% per year indefinitely. If last year’s dividend was $1 and the required return is 20%, what is the price of the stock?
  • Compute the dividends until growth levels off
    • D1 = 1(1.2) = $1.20
    • D2 = 1.20(1.15) = $1.38
    • D3 = 1.38(1.05) = $1.449

• Find the expected future price of dividends starting in Year 3
  • P2 = D3 / (R – g) = $1.449 / (.2 – .05) = $9.66

• Find the present value of the expected future cash flows
  • P0 = $1.20 / (1.2) + ($1.38 + 9.66) / (1.2)2 = $8.67

Stocks that Don’t Pay Dividends

• Many firms do not pay dividends: Apple, Google, Amazon
• Are the shares of these firms worthless?
  • No – instead of paying dividends, they plowback cash flow into internal projects

• For a stock that currently pays no dividend, market value derives from
  • Hope of future dividends, and/or
  • Expectation of a liquidating dividend
• Our valuation models only say that dividends cannot be zero in all periods

Required Returns

•  Dividend growth model sheds light on required return

• Rearrange and solve for R

• Total return has two parts
  • Dividend yield (D1/P0) – return from dividend next period
  • Capital gain yield (g) – rate at which value of investment grows

Required Return: Example

• A firm’s stock is selling for $10.50. It just paid a $1 dividend and dividends are expected to grow at 5% per year.

• What is the required return?
  • R = D1/P0 + g
  • R = [$1 x (1.05)/$10.50] + .05 = 15%

• What is the dividend yield?
  • Dividend yield = D1/P0
  • Dividend yield = $1.05 / $10.50 = 10%

• What is the capital gains yield?
  • Capital gain yield = g = 5%

Other methods to consider…. here.

Current Value of a Stock

• We covered special cases that allow us to value stocks
• As with bonds, numerous factors influence price of stock
  • Large fluctuations in value of stocks (even over short periods)
• Current value of stock determined by the market
  • Constantly changing as new information arrives and investors reassess firm’s future cash flows and risks
• Easiest way to find current value is the Internet
  • finance.google.com or finance.yahoo.com

Wrap-Up

• Stock represents ownership stake in the firm
• Stock price is the present value of all expected future dividends
• Required return is sum of dividend yield and capital gain

For more classes:

Education Series