When I mention options investing, I usually get one of two responses. The first is concern: “Options? Aren’t those like super leveraged derivatives? What are you, a gambler?!”
Options have a bad reputation, and for good reason. After all, our friends at Wall Street Bets have taken over and turned the options market into a casino. But just like options can be used for gambling, they can also be used to structure risk and formulate payoffs that have the potential to reduce risk at the portfolio level. In fact, options are one of the best tools at our disposal to manage portfolio risk, if used correctly.
So if concern is the first reaction I get, the second is usually confusion. That is because options can get pretty complicated, pretty quick. Valuing options can also be a huge headache. Even the terms can sound dreadful: “Black-Scholes-Merton? Put-Call Parity? Binomial Tree Models? What is going on?!” But fear not! Here at Alpha Architect our number one goal is to empower investors through education, and that’s what I’ll do today. In this post, we’ll go over the basics of options so that you, too, can understand them.
Let’s dive in.
What is an option?
To simplify things, we’re first going to discuss call options. Then, we’ll move to put options.
A call option is a contract where the option buyer has the right to buy an underlying from the option seller at a pre-specified price on or by a pre-specified date.
Simply put (no pun intended), when you buy a call, you are buying the right, but not the obligation, to purchase an underlying at a certain price by a certain date. Obviously if you have the right to something, you must pay for that right. So, here’s the first rule of options:
Rule #1: Buyers pay sellers a specified premium for an option.
Makes sense, right?
So if the buyer has the right but not the obligation, the seller must have the exact opposite payoff structure.
In a call, the seller has the obligation to sell the underlying to the buyer if the buyer decides to exercise the option by or on the expiration date.
As you can see, options are a zero-sum-game. Transaction costs aside, one party must lose what the other party wins.
The Expiration Date
This right that the buyer has purchased is not perpetual. It expires on a certain date and time. This is called the expiration date, which is the last day an option can be exercised. When an option is exercised, the buyer has enforced his right to buy the underlying, so the seller has to deliver the underlying right when the buyer exercises the option.
Now, it’s important to note when options can be exercised. If an option can be exercised before the expiration date, this is what we call an American-style option. And no, this has nothing to do with geography. On the other hand, if an option can only be exercised upon expiration, that is what we call a European-style option.
This distinction is important when it comes to specific strategies that need to avoid early exercise risk. But in general, investors do not exercise options before the expiration date since they can simply sell. If an investor were to exercise an option before expiration instead of selling, he is giving up on the time value of money. See, because the buyer has purchased an option, part of the value of that option, and part of the price the buyer paid for, is for the amount of time the buyer has before expiration. The more time between now and expiration, the more the buyer should pay. When a buyer exercises the option before expiration, they are giving up that time value, however big or small. Usually, if a buyer is ready to close the position, it is likely more favorable for the buyer to simply sell the position instead of exercising it.
Lastly, let’s talk about the pre-specified or strike price.
The Strike Price
The strike price is the agreed-upon price at which the call option buyer can buy the underlying.
Let’s put this in perspective.
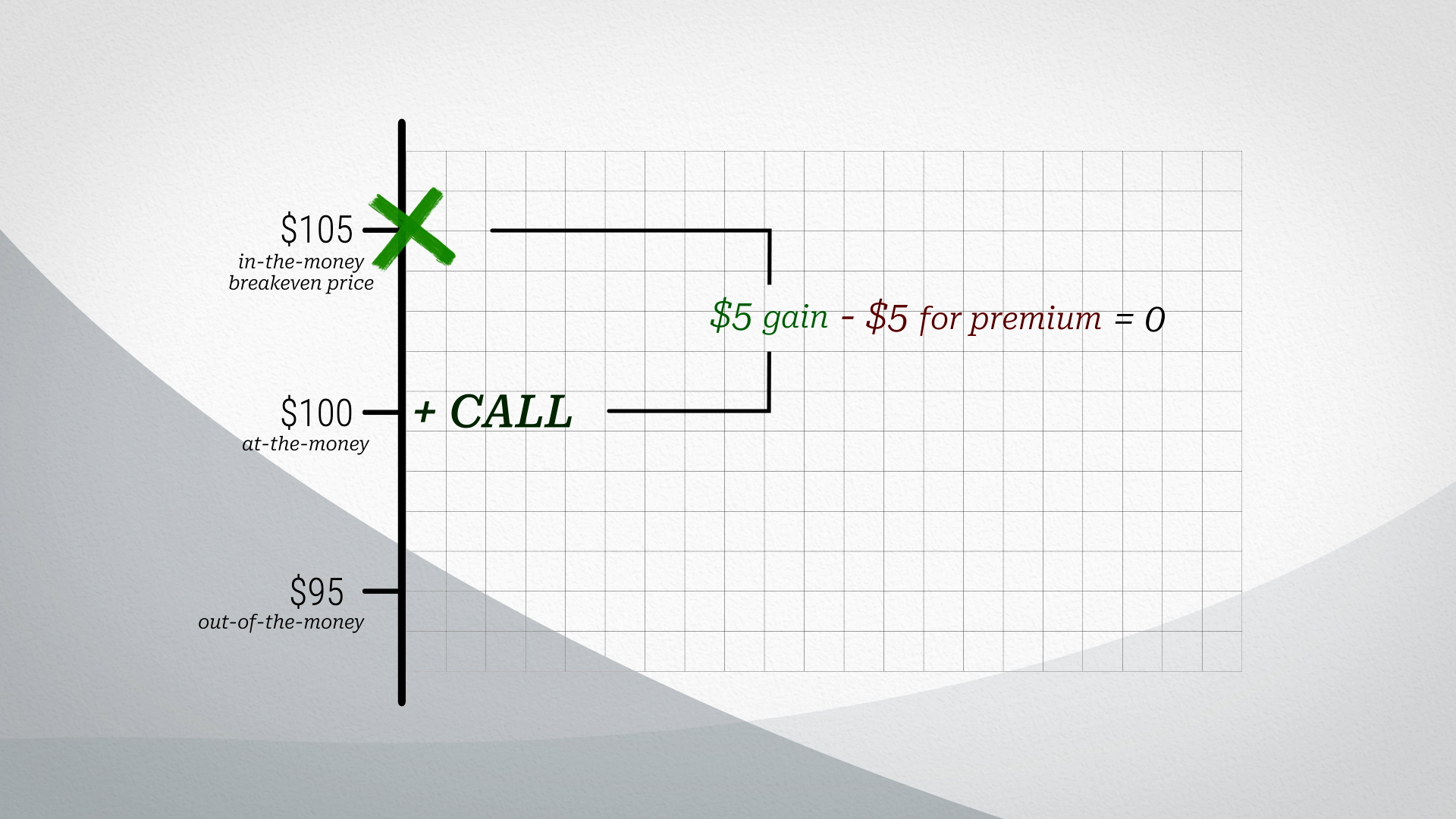
Let’s say that you buy a call on a stock, currently trading at $100. You buy the option with six-months left to expiration at a strike price of $100. Since the underlying is trading at $100, and your strike is at $100, you have bought an option that is at-the-money.
If the stock were to drop to $95, you are now out-of-the-money, which simply means that exercising the option would make no economic sense. You would be paying $100 for something that you could buy in the market for $95.
If the stock were to jump up to $105, the option is in-the-money; which means that you could theoretically exercise the option at a gain, since you can buy something that is currently trading at $105 for $100.
Although in this example the value of the option is a gain of $5, the profit of the buyer will likely be less than $5, since, remember, the buyer must have paid a premium to enter into the option contract.
Let’s say the option buyer paid $5 for the option premium, and the stock is trading at $105. Even though the value of the option is $5, the option cost the buyer $5, so the option buyer is just breaking even.
On the other hand, the seller has not lost any money on the contract, since he’s received $5 of premium and must pay $5 on the value of the option.
$105, therefore, is what we call the break-even-price.
Put Options
So far we’ve only talked about call options, which give the buyer the right to purchase an underlying. If an investor buys a call, he will benefit from appreciation in the underlying. Therefore, we can think of the investor as bullish.
The other type of option is a put option, which is a contract where the option buyer has the right to sell an underlying to the option seller at a pre-specified price on or by a pre-specified date.
If an investor buys a put, he will benefit from depreciation in the underlying. Therefore, we can think of the investor as bearish.
Let’s use our past example, but flip the tables so that the option buyer is a put buyer.
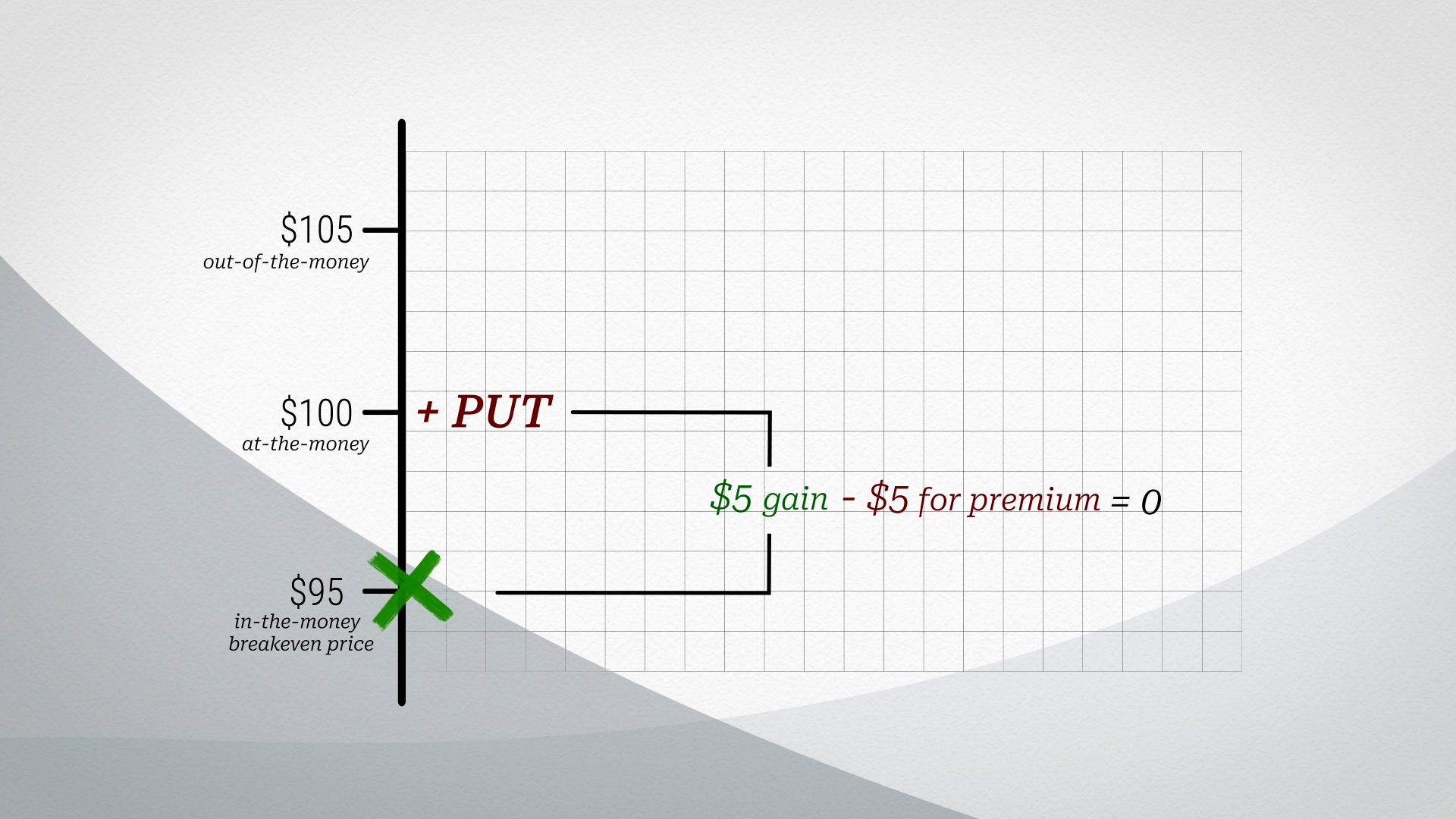
Let’s say that you buy a put on a stock, currently trading at $100. You buy the option with six-months left to expiration at a strike price of $100. Since the underlying is trading at $100, and your strike is at $100, you have bought an option that is at-the-money.
If the stock were to jump up to $105, the option is out-of-the-money, which simply means that exercising the option would make no economic sense. You would be selling a stock that is currently trading at $105 for $100.
If the stock were to drop to $95, you are now in-the-money. You could theoretically exercise the put option at a gain, since you can sell something that is trading at $95 for $100.
Although in this example the value of the option is $5, the profit of the put buyer will likely be less than $5, since, remember, the buyer must have paid a premium for the option. If the option buyer paid $5 for the option premium and the stock is trading at $95, even though the value of the option is $5, the put option cost the buyer $5, so the option buyer is just breaking even.
On the other hand, the seller has not lost any money on the contract, since he’s received $5 of premium and has lost $5 on the value of the put option. $95, therefore, is what we call the break-even-price.
Which leads me to the second rule of options:
Rule #2: Long calls and short puts benefit from appreciation of the underlying. Long puts and short calls benefit from depreciation of the underlying.
Let’s dive deeper and break down the potential payoffs from each of our four options:
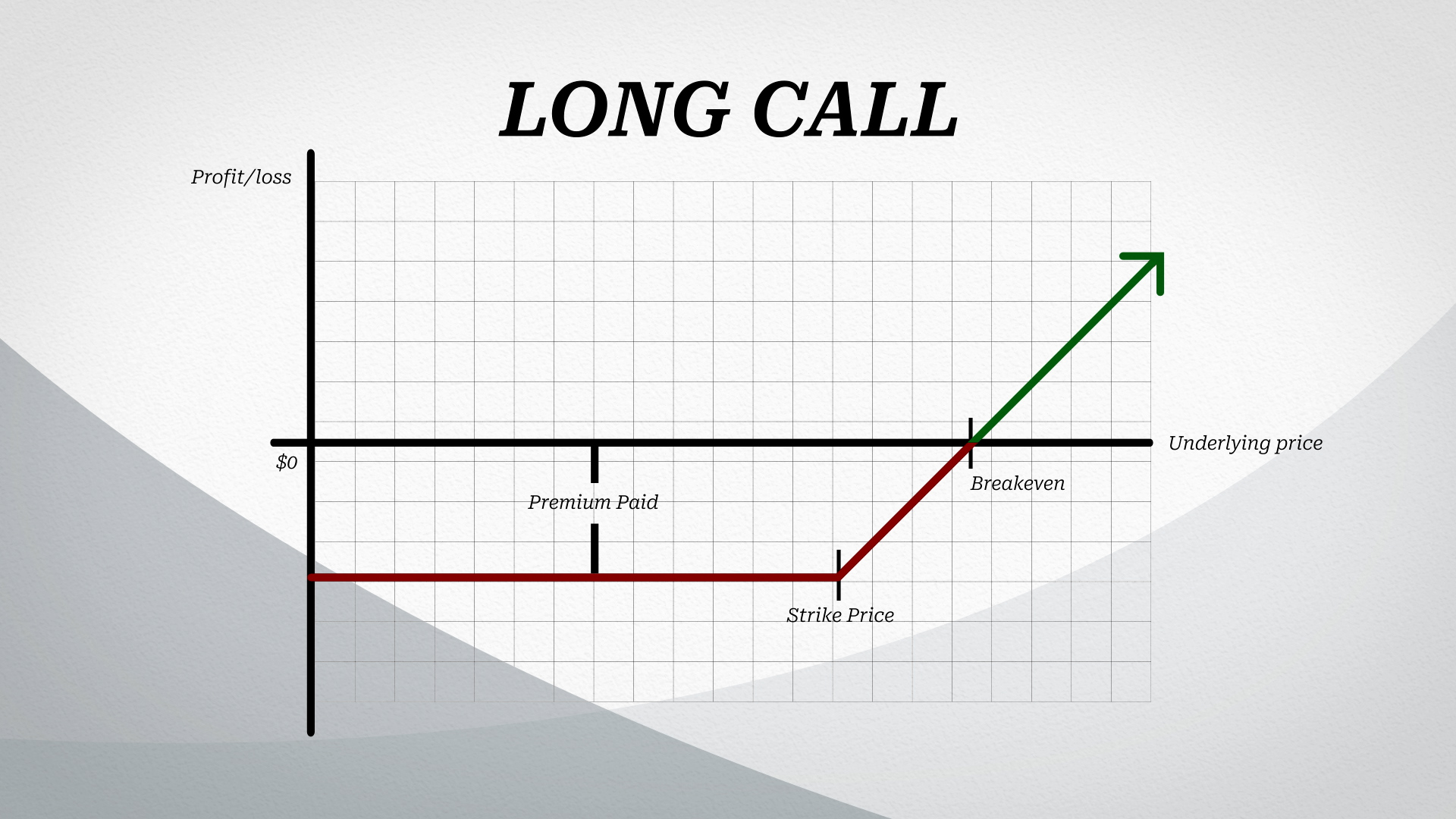
The Long Call: Upon entering the position, buyers incur an initial loss since they must pay a premium to the seller to initiate the contract. However, that’s all they can lose. Conversely, the potential gains are virtually unlimited because the underlying could continue rising indefinitely.
A long call, then, has theoretical infinite gains and capped losses.
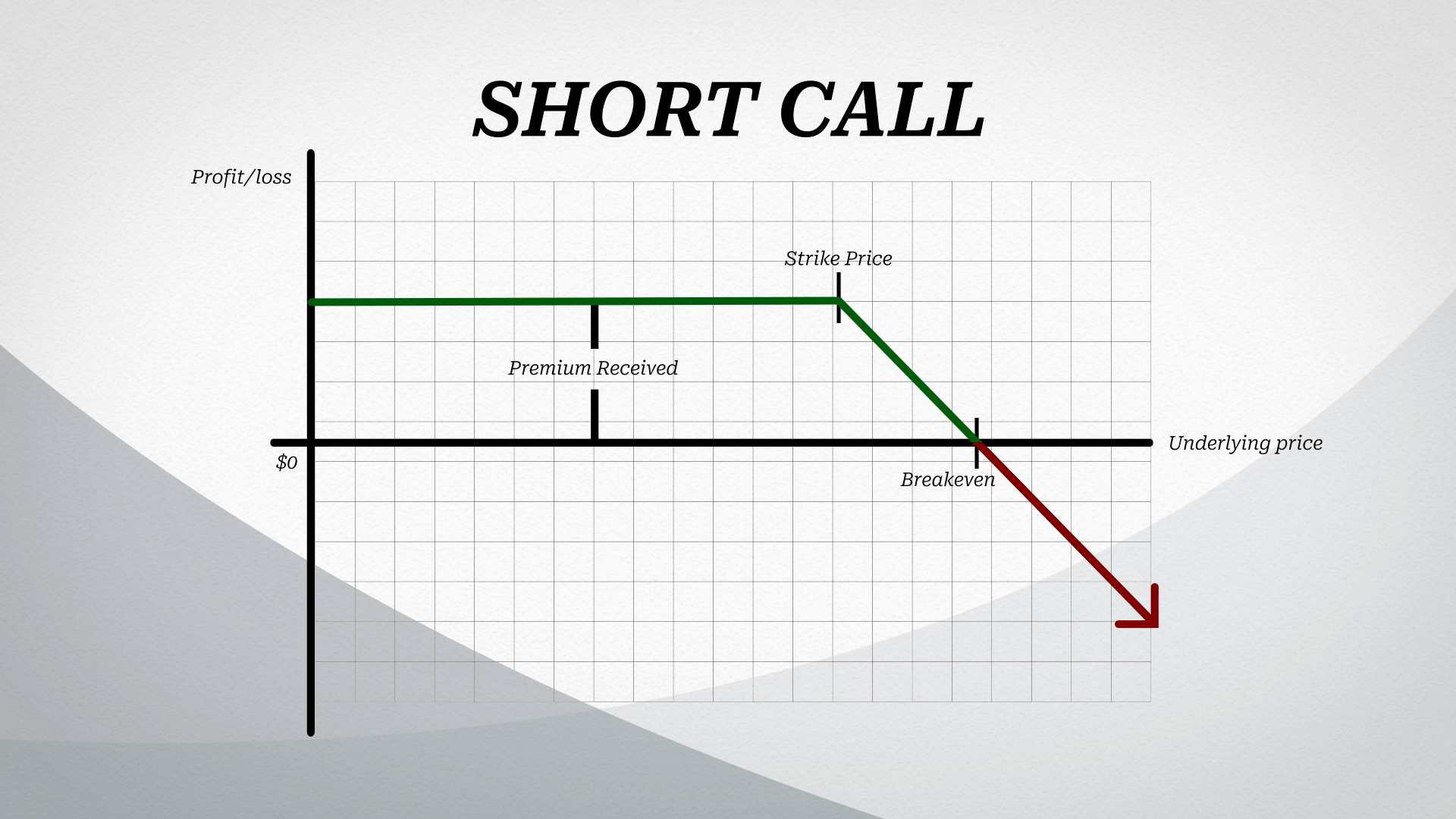
The Naked Short Call: We’re going to be talking about a naked short call, meaning the seller of this option has no offsetting collateral.
Upon entering the position, sellers gain from the premium received. However, the underlying could rise indefinitely and produce theoretically infinite losses. Notice how this is the exact mirror opposite of the long call. It has capped gains and theoretical infinite losses.
The Long Put: Upon entering the long put position, buyers pay a premium to the seller, which represents the maximum loss for the buyer. As the option moves into the money, however, the buyers begin garnering return. Unlike the long call, however, these profits are not theoretically infinite because the underlying can simply go to zero. The max profit of the long put buyer would then be the difference between the strike price and zero, minus any premium paid.
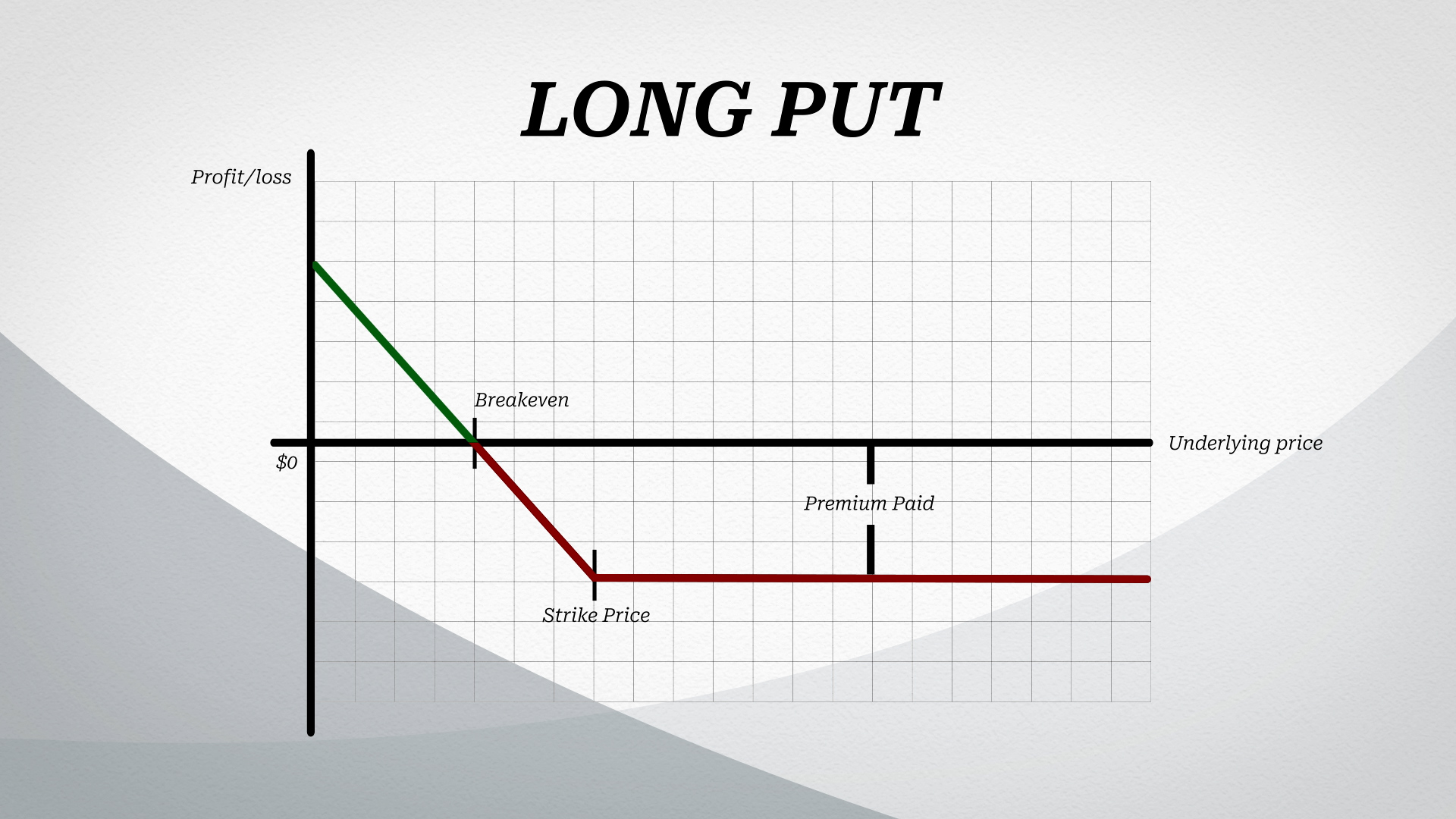
The Naked Short Put: Upon entering the position, sellers gain from the premium received. However, as the underlying starts moving into the money, the put seller can experience significant losses. Unlike the call seller, however, the put seller does not have theoretical infinite losses since the underlying would stop trading at zero. Still, these losses can be substantial.
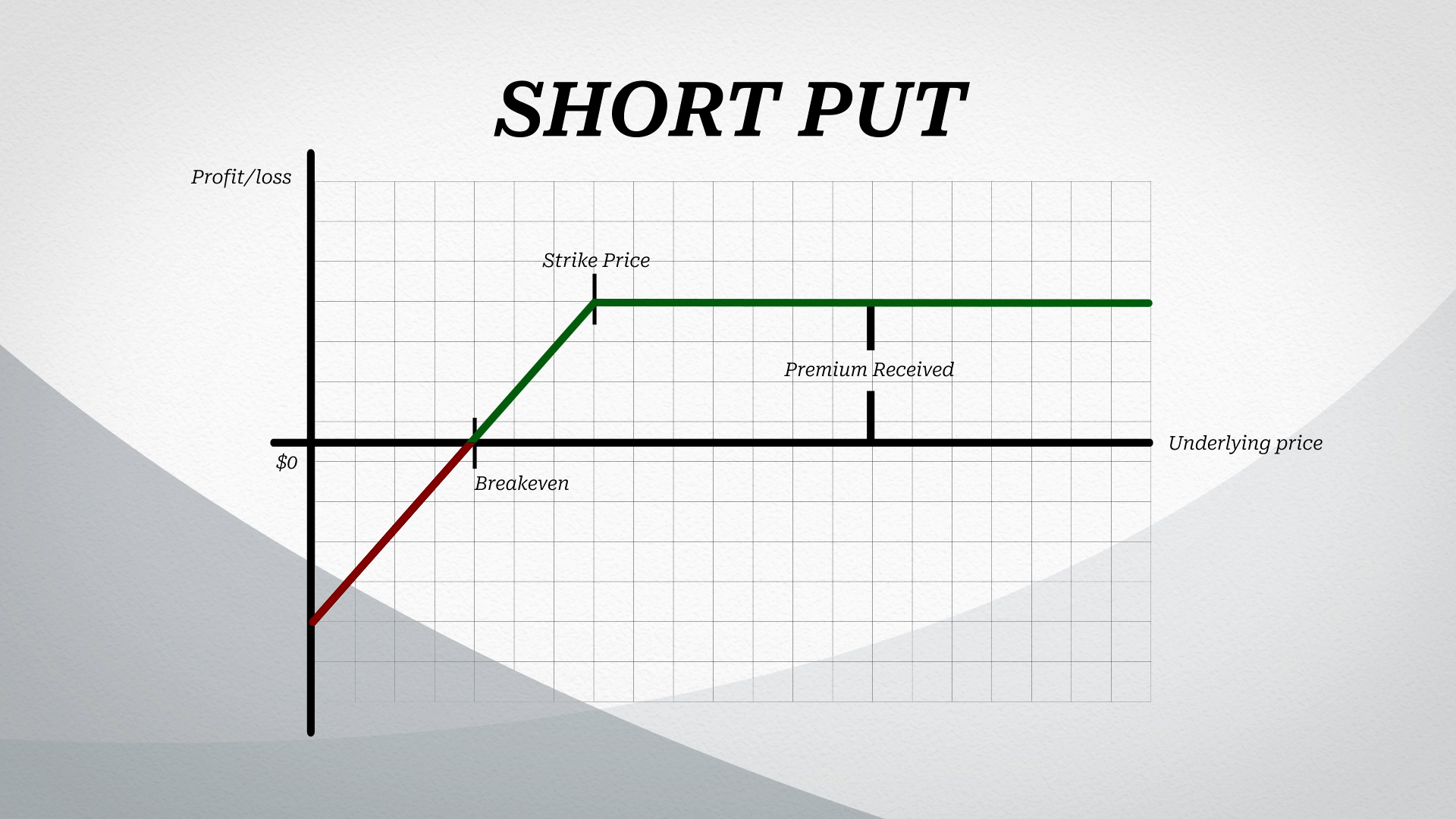
You can see a developing theme here: being long options gives investors a small probability of receiving truly explosive returns. Being naked short options can give investors probable, small, and defined gains, but can also explode if the underlying moves against them.
Which leads me to the third and last rule of options for this blog post:
Rule #3: The more unlikely a payoff is, the higher the payoff amount.
This should make intuitive sense. If an option position is likely to expire out-of-the-money, it should be cheap to purchase. On the other hand, if it does pay off, it better yield a huge payout.
Let’s dig deeper as to why this is the case.
Let’s say a stock is trading at $100 and you have reason to believe that the stock will drop. There are two put options you are eyeing, both expiring in three months:
1) A $90-strike put, each selling for $4.
2) A $30-strike put, each selling for $0.01.
Remember, these prices should make sense because it’s more probable for the stock to drop $10 than it is to drop $70.
You have a $12 budget, so now you have a choice to make: Do you purchase 3 options at a $90 strike, or do you purchase 1,200 options at a $30 strike? What about a mix of both?
Well, if you were to purchase the 3 options at a $90 strike, your max profit would be $258. That is $270 ($90 max gain per option x 3 options) – $12 paid for the premium. Not bad.
But if you bought the $30 strike, your max profit would be a whopping $35,988. That is $36,000 ($30 max gain per option x 1,200 options) – $12 paid for the premium.
Now you can start seeing the power of the embedded leverage in options.

It’s important to understand that the $30 strike is cheap because it is so unlikely that this payoff would ever happen.
This is all due to something called convexity, which is best thought of as non-linearity.
For a highly convex option position, as the underlying changes, the price of the option doesn’t change linearly, but accelerates as the underlying price changes.
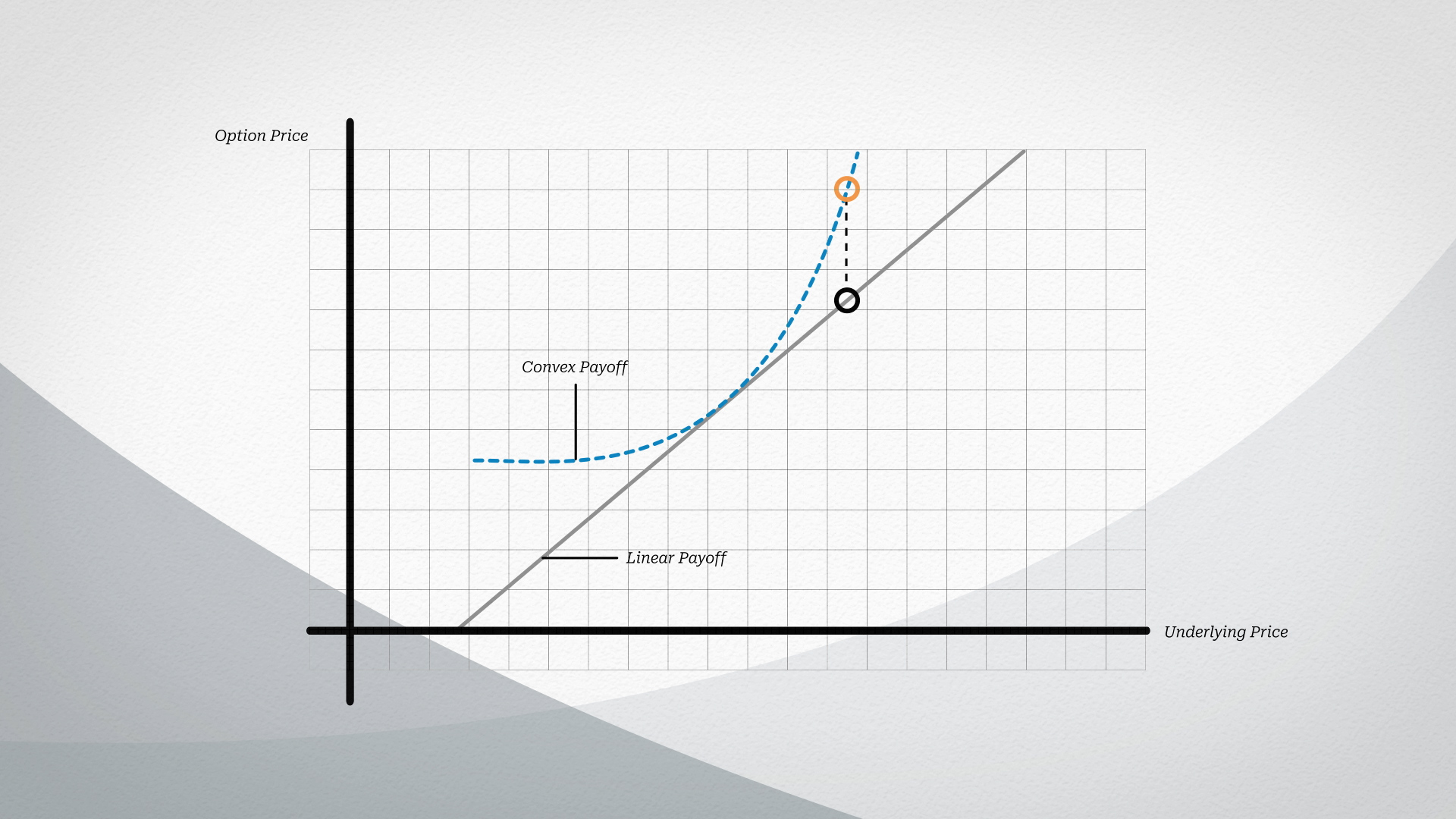
These convex payoffs especially occur when options move from far out-of-the-money to in-the-money. Additionally, the closer to expiration an option is, the greater the convexity.
Convexity, then, is the key to achieving explosive payoffs from unlikely events.
That’s it for today! I hope you enjoyed and learned from this walkthrough. If you did, make sure to watch the video version and subscribe to the Alpha Architect YouTube channel for content to come.
Godspeed!
About the Author: Jose Ordonez
—
Important Disclosures
For informational and educational purposes only and should not be construed as specific investment, accounting, legal, or tax advice. Certain information is deemed to be reliable, but its accuracy and completeness cannot be guaranteed. Third party information may become outdated or otherwise superseded without notice. Neither the Securities and Exchange Commission (SEC) nor any other federal or state agency has approved, determined the accuracy, or confirmed the adequacy of this article.
The views and opinions expressed herein are those of the author and do not necessarily reflect the views of Alpha Architect, its affiliates or its employees. Our full disclosures are available here. Definitions of common statistics used in our analysis are available here (towards the bottom).
Join thousands of other readers and subscribe to our blog.

