The Law of Large Numbers and Casino Earnings

“…Even the stupidest man knows by some instinct of nature…that the greater the number of confirming observations, the surer the conjecture.”
– Jacob Bernoulli

In statistics, you can analyze a sample from a population, and reach general conclusions about the population based on the sample. Because the sample is only a part of the whole, however, and the sampling is affected by luck in various ways, there is always the chance that the sample does not accurately represent the whole. Bernoulli was able to quantify that chance. Bernoulli made his famous observations about this in the 18th century, in his work, “Ars Conjectandi” (the art of conjecturing).

In Against the Gods: The Remarkable Story of Risk the author, Peter Bernstein, provides a brief overview of Bernoulli’s Law of Large Numbers:

“Suppose you toss a coin over and over. The Law of Large Numbers does not tell you that the average of your throws will approach 50% as you increase the number of throws; simple mathematics can tell you that, sparing you the tedious business of tossing the coin over and over. Rather, the law states that increasing the number of throws will correspondingly increase the probability that the ratio of heads thrown to total throws will vary from 50% by less than some stated amount, no matter how small. The word “vary” is what matters. The search is not for the true mean of 50% but for the probability that the error between the observed average and the true average will be less than, say, 2% – in other words, that increasing the number of throws will increase the probability that the observed average will fall within 2% of the true average.

That does not mean that there will be no error after an infinite number of throws; Jacob explicitly excludes that case. Nor does it mean that the errors will of necessity become small enough to ignore. All the law tells us is that the average of a large number of throws will be more likely than the average of a small number of throws to differ from the true average by less than some stated amount.”

Below is a graphic depiction of the Law of Large Numbers in action, with 10 separate coins flipped 1,000 times each:

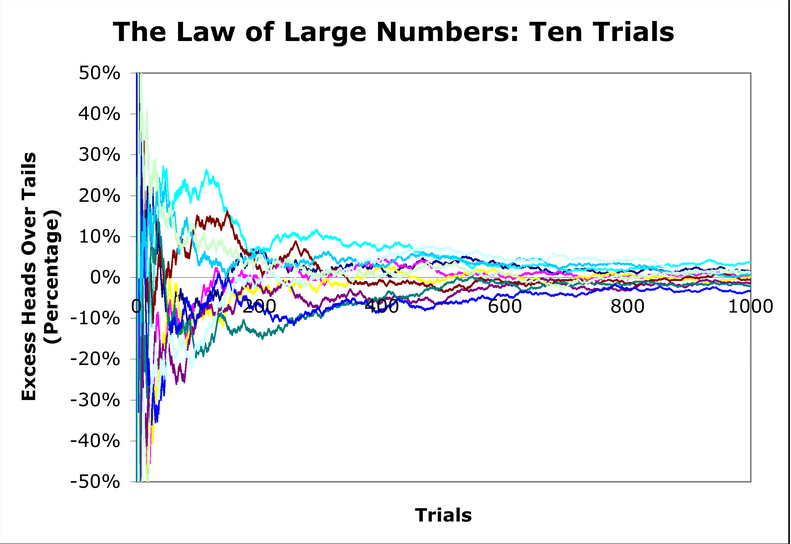
Coin flips are interesting theoretically, but the Law of Large numbers has a number of practical implications in the real world.

Casinos, for example, live and die by the law of large numbers. Each game has a house edge built into it, representing the average loss over the initial bet. Some sample edges:

• Blackjack – 0.75%
• Baccarat – 1.2%
• Craps – 1.4%
• Roulette – 5%
• Slot machines – 5-10%

As Bernoulli pointed out, over longer and longer time frames, it becomes increasingly likely that the house edge will represent the casino’s profit margin. There can, however, be hiccups along the way to long-run profitability.

A few years ago, I had a friend (I’ll call her “Susan”) who worked at a large bank. She was very good with numbers, and the bank would send her out in a sort of utility role, for instance when they had a client with an unusual request. One day, Susan was sent out to a large casino client. The bank had loans out to the casino, which was a reliable money maker over the long run (due to the Law of Large Numbers) but the casino had a risk management problem they wanted help with.

The casino catered to “whales,” which were rich, high-rollers who came and bet huge sums at the tables. The casino would comp them rooms and meals and so forth, and even fly them out, in order to entice them to place their big bets. This occasionally presented a problem for the casino. Though the whales were profitable in the long run, sometimes they would come to the casino and win, sometimes very big. The effect of these big wins was so great at times that it materially affected the GAAP earnings for the casino, which was a public company. The managers didn’t like that volatility and wanted to do something about it.

Susan created a win/win, by selling the casino a swap insuring the casino against the volatility caused by whales. The bank became the counter-party for the volatile cash flows resulting from the whales’ big wins and the losses, but would pay out a stable return based on whales’ betting and the long-run profit expectations associated with the house edge, but at discount that reflected the cost of the swap.

This particular story has a happy ending for both the casino and the bank, but of course, it’s still up to the casino not to do anything stupid when hosting whales, who may find ways to challenge the house edge at the margin. The following link describes how the U.S. poker pro Phil Ivey won $12 million from Crockfords, Britain’s oldest private gambling clubs: http://www.grantland.com/blog/the-triangle/post/_/id/62856/the-curious-case-of-poker-pro-phil-iveys-punto-banco-rake

With guys like Phil Ivey working on your house edge, casinos are clearly difficult businesses to risk manage. We’ll stick to quant investing!

If you’d like to further investigate how insurance and casinos harness their edge, I encourage you to explore the spreadsheet Wes presents in his lectures at Drexel:

diversification

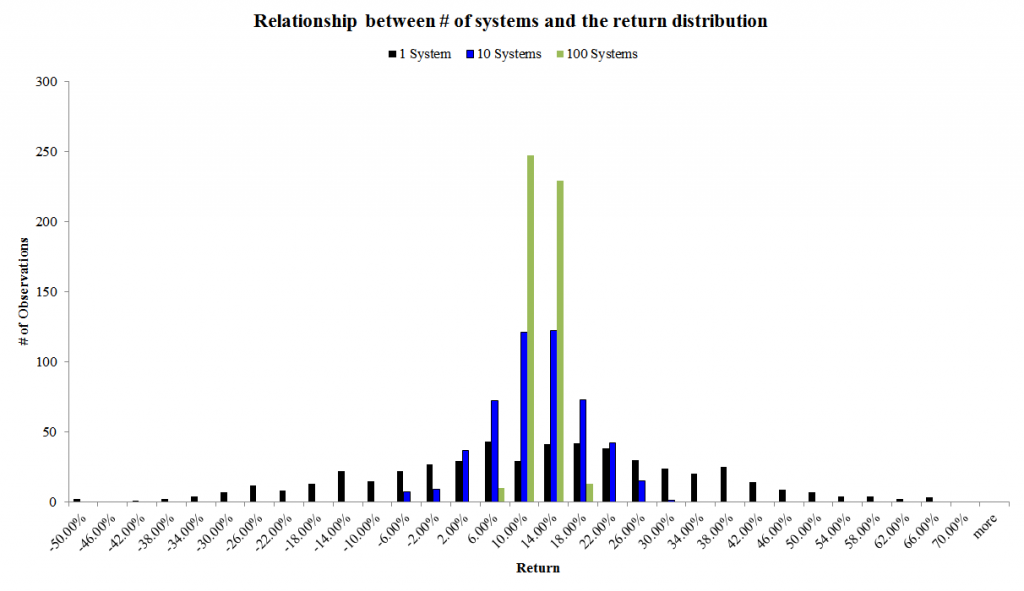
The spreadsheet conducts a 1000 simulations. In each simulation run, a system can either take 1 bet, 10 bets, or 100 bets–all uncorrelated. As the chart above suggests, one can manage risk by pooling truly uncorrelated bets together. As the number of bets increases, the volatility goes to zero and the expected value becomes the observation.

Thoughts on gambling?