Introduction to Finance: Class 5
Net Present Value & Other Investment Criteria
What is net present value?
The difference between the present value of cash inflows and the present value of cash outflows. NPV is used in capital budgeting to analyze the profitability of an investment or project.
—Source
· · · · ·
Key Concepts:
- Review: Corporate Finance
- Good Decision Criteria for Capital Budgeting
- Net Present Value
- Payback Rule
- Accounting Rates of Returns
- Internal Rate of Return
Corporate Finance
- Corporate Finance helps us answer the following types of questions:
- What long-term investments should your firm take on?
- Should you purchase a new grill that makes better steaks?
- Should you open another shop across town?
- Where will you get the money to pay for you investments?
- Will you borrow it?
- Will you encourage others to invest in the firm?
- How will you manage the firm’s day-to-day financial activities?
- How much cash should you keep in the bank?
- Should you pay your suppliers in cash or on credit?
- Corporate finance is the study of financial decision making
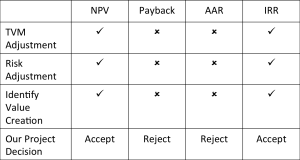
Good Decision Criteria for Capital Budgeting
- We need to ask ourselves the following questions when evaluating decision criteria:
- Does the decision rule adjust for the time value of money?
- Does the decision rule adjust for risk?
- Does the decision rule provide information on whether we are creating value for the firm?
- Remember goal of Corporate Finance…
- Create value over long-term for owners of a project
- Value Creation: Market Value of Project > Cost to Acquire
- Example
- Buy run down house for $25K
- Spend another $25K on painters, plumbers, etc. to fix it up
- Sell house for $60K
→Market value ($60K) > cost ($50K) by $10K
- Created $10K in value by bringing together fixed asset (house), labor (plumbers, etc) and materials (carpet, paint, etc.)
Net Present Value
- Best decision criteria
- The Net Present Value of a project is the difference between its market value and its cost
- NPV tells us how much value is created from undertaking an investment
- Three step process:
- Estimate the expected future cash flows
- Estimate the required return for projects with this risk level
- Find the present value of the future cash flows and subtract the initial investment
Net Present Value Decision Rule
- An investment should be accepted if the NPV is positive and rejected if the NPV is negative
- A positive NPV means that the project is expected to add value to the firm and will therefore increase the wealth of the owners
- Since our goal is to increase owner wealth, NPV is a direct measure of how well this project will meet our goal
- Decision Criteria Test: Satisfied
- Decision rule adjusts for the time value of money
- Decision rule adjusts for risk
- Decision rule provides information on whether we are creating value for the firm
- NPV decision rule is a candidate for our primary decision rule
Example: Computing NPV
- You are looking at a new project and you have estimated the following cash flows and net income:
- Year 0: CF = -165,000
- Year 1: CF = 63,120; NI = 13,620
- Year 2: CF = 70,800; NI = 3,300
- Year 3: CF = 91,080; NI = 29,100
- Your required return for assets of this risk is 12%
- The average book value of the project is 72,000
- Find Present Value of estimated future cash flows
- PV = 63,120/(1.12) + 70,800/(1.12)^2 + 91,080/(1.12)^3
- PV = 177,627
- Subtract cost of initial investment
- NPV = PV – Initial Cost
- NPV = 177,627 – 165,000
- NPV = 12,627
Payback Rule
- Payback period is the length of time if takes to recover your initial investment
- Computation
- Estimate the cash flows
- Subtract the future cash flows from the initial cost until the initial investment has been recovered
Payback Period Decision Rule
- Accept project if its calculated payback period is less than some preset number of years
- Decision Criteria Test: Unsatisfied
- Decision rule adjusts for the time value of money
- Decision rule adjusts for risk
- Decision rule provides information on whether we are creating value for the firm
- NPV decision rule is a candidate for our primary decision rule
Example: Computing Payback Period
- You are looking at a new project and you have estimated the following cash flows and net income:
- Year 0: CF = -165,000
- Year 1: CF = 63,120; NI = 13,620
- Year 2: CF = 70,800; NI = 3,300
- Year 3: CF = 91,080; NI = 29,100
- Your required return for assets of this risk is 12%
- The average book value of the project is 72,000
- Assume we will accept the project if it pays back within two years
- Year 1: 165,000 – 63,120 = 101,880 still to recover
- Year 2: 101,880 – 70,800 = 31,080 still to recover
- Year 3: 31,080 – 91,080 = -60,000 project pays back during year 3
- Payback = 2 years + 31,080/91,080 = 2.34 years
- Do we accept or reject the project based on the payback period rule?
Advantages & Disadvantages of Payback
- Advantages
- Easy to understand
- Adjusts for uncertainty of later cash flows
- Biased towards liquidity
- Disadvantages
- Ignores the time value of money
- Requires an arbitrary cutoff point
- Ignores cash flows beyond the cutoff date
- Biased against long-term projects, such as research and development, and new projects
Accounting Rates of Returns
- Average Accounting Return = Average Accounting Profit / Average Accounting Value
- Computation in Book
- AAR = Average net income / Average book value
- Need to have a target cutoff rate
Average Accounting Return Decision Rule
- Accept project if its average accounting return exceeds a target average accounting return
- Decision Criteria Test: Unsatisfied
- Decision rule adjusts for the time value of money
- Decision rule adjusts for risk
- Decision rule provides information on whether we are creating value for the firm
- NPV decision rule is a candidate for our primary decision rule
Example: Computing AAR
- You are looking at a new project and you have estimated the following cash flows and net income:
- Year 0: CF = -165,000
- Year 1: CF = 63,120; NI = 13,620
- Year 2: CF = 70,800; NI = 3,300
- Year 3: CF = 91,080; NI = 29,100
- Your required return for assets of this risk is 12%
- The average book value of the project is 72,000
- Assume we require an average accounting return of 25%
- Average Net Income:
- ($13,620 + 3,300 + 29,100) / 3 = $15,340
- Average Book Value: $72,000
- AAR = $15,340 / 72,000 = .213 = 21.3%
- Do we accept or reject the project based on the average accounting return rule?
Advantages & Disadvantages of AAR
- Advantages
- Easy to calculate
- Needed information will usually be available
- Disadvantages
- Not a true rate of return; time value of money is ignored
- Uses an arbitrary benchmark cutoff rate
- Based on accounting net income and book values, not cash flows and market values
Internal Rate of Return
- Internal rate of return is the discount rate that makes the NPV of the project = $0
- IRR tells us how high the discount rate would need to be before a project is unacceptable
- “Internal” because based entirely on estimated cash flows and is independent of interest rates found elsewhere
Internal Rate of Return Decision Rule
- An investment should be accepted if its internal rate of return exceeds the required return. Otherwise, it should be rejected
- Goal of IRR analysis is to find a range of discount rates for which a project is acceptable
- IRR tells us the discount rate that makes the project simply break even (NPV=$0)
- Remember: A decrease in the discount rate increases the present value of future cash flows
- Thus, if the actual discount rate (or required return) is less than the IRR, then the project will create value
- Decision Criteria Test: Satisfied
- Decision rule adjusts for the time value of money
- Decision rule adjusts for risk
- Decision rule provides information on whether we are creating value for the firm
- NPV decision rule is a candidate for our primary decision rule
Example: Computing IRR
- You are looking at a new project and you have estimated the following cash flows and net income:
- Year 0: CF = -165,000
- Year 1: CF = 63,120; NI = 13,620
- Year 2: CF = 70,800; NI = 3,300
- Year 3: CF = 91,080; NI = 29,100
- Your required return for assets of this risk is 12%
- The average book value of the project is 72,000
Single Period Projects
- Suppose a project costs $100 today and has an estimated cash flow of $110 next year
- If the required return is 12%, should we accept this project based on the IRR decision rule?
- Find the discount rate that sets NPV = $0
- NPV = -$100 + $110 / (1+r) = $0
- r = 110 / 100 – 1 = 10%
- IRR = 10%
- Since IRR < required return → Reject project
Advantages & Disadvantages of IRR
- Advantages
- NPV and IRR will generally give us the same decision
- Knowing a return is intuitively appealing
- It is a simple way to communicate the value of a project to someone who doesn’t know all the estimation details
- If the IRR is high enough, you may not need to estimate a required return, which is often a difficult task
- Disadvantages
- IRR decision rule is unreliable in the following situations
- Nonconventional cash flows
- Cash flow signs change more than once
- Mutually exclusive projects
- Initial investments are substantially different
- Timing of cash flows is substantially different
- Nonconventional cash flows
- IRR decision rule is unreliable in the following situations
IRR: Nonconventional Cash Flows & Mutually Exclusive Projects
Nonconventional Cash Flows
- When the cash flows change signs more than once, there is more than one IRR
- Mathematically, when you solve for IRR, you are solving for the root of an equation and when you cross the x-axis more than once, there will be more than one return that solves the equation
- If you have more than one IRR, which one do you use to make your decision?
Example: Nonconventional Cash Flow
- Suppose an investment will cost $90,000 initially and will generate the following cash flows:
- Year 1: $132,000
- Year 2: $100,000
- Year 3: -$150,000
- The required return is 15%
- Should we accept or reject the project?
- NPV = -90K + 132K / 1.15 + 100K / (1.15)^2 – 150K / (1.15)^3
- NPV = $1,769.54 → Accept
- IRR = 10.11% < 15% → Reject
Mutually Exclusive Projects
- If you choose one, you can’t choose the other
- Intuitively, you would use the following decision rules:
- NPV – choose the project with the higher NPV
- IRR – choose the project with the higher IRR
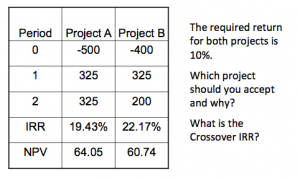
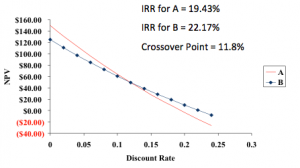
Example: Mutually Exclusive Projects
· · · · ·
Test Your Knowledge (answers found below)
- An investment project has an initial cost of $1M today and will generate cash flows of $200K per year over the next eight years
- If discount rate is 12% and required payback is 3 years, should we accept or reject this project based on the following decision rules:
- Net present value
- Payback period
- Internal rate of return
Wrap-Up
- NPV rule is primary decision rule
- If a project has a positive NPV, it creates value for owners of the project and should be accepted
- If you have two mutually exclusive projects, choose the one with the higher NPV
- Although flawed, IRR, payback period, and average accounting return also used in practice
- Summary of Decision Rules
- NPV vs. IRR
- NPV directly measures the increase in value to the firm
- Whenever there is a conflict between NPV and another decision rule, you should always use NPV
- IRR is unreliable in the following situations
- Non-conventional cash flows
- Mutually exclusive projects
- Capital Budgeting in Practice:
- We should consider several investment criteria when making decisions
- NPV and IRR are the most commonly used primary investment criteria
- Payback is a commonly used secondary investment criteria
- 1999 survey of 392 chief financial officers at large and small firms in the U.S.
- IRR and NPV are the two most widely used techniques
- Among smaller firms, payback is used as much as NPV & IRR
· · · · ·
Solutions
- Investment Project
- Cost: $1M today
- Cash Inflows: $200K / YR for 8 years
- Discount Rate: 12%
- Accept or Reject?
- Net present value
- NPV = -$1M + $200K x [1 – 1/(1.12)^8] / 0.12
- NPV = -$6,472.05
- NPV < 0 → Reject
- Net present value
- Payback period
- Required payback is 3 years
- Actual payback = $1M / $200K = 5 years
- Payback Period > Required Payback → Reject!
- Internal rate of return
- -$1M + $200K x [1 – 1/(1+r)^8]/r = $0
- IRR; CPT IRR = 11.81%
- IRR < Required Return → Reject!
- IRR is discount rate that sets NPV=$0
- Required return (or discount rate) above the IRR → NPV < $0
For more classes:
Education Series
About the Author: Victoria Tran
—
Important Disclosures
For informational and educational purposes only and should not be construed as specific investment, accounting, legal, or tax advice. Certain information is deemed to be reliable, but its accuracy and completeness cannot be guaranteed. Third party information may become outdated or otherwise superseded without notice. Neither the Securities and Exchange Commission (SEC) nor any other federal or state agency has approved, determined the accuracy, or confirmed the adequacy of this article.
The views and opinions expressed herein are those of the author and do not necessarily reflect the views of Alpha Architect, its affiliates or its employees. Our full disclosures are available here. Definitions of common statistics used in our analysis are available here (towards the bottom).
Join thousands of other readers and subscribe to our blog.