Backtesting strategies based on multiple signals — Beware of Overfitting Bias!

One of the dangers of being a quantitative investor is that when you see patterns in historical data you might wrongly assume they will repeat. Put another way, you might believe an effect is driven by a genuine relationship when in reality the results are spurious and the result of luck. We wrote here about “anomaly chasing” and the risks of data mining in backtests.

A responsible researcher has the tools to address this risk. The “gold standard,” of course, is to review out-of-sample results. In the absence of out-of-sample data, a skeptic might look for a high degree of statistical significance.

Unfortunately, t-statistics are not a silver bullet, and sometimes should be taken with a grain of salt. This is especially true when you are optimizing on or weighting groups of signals that perform the best together, even though they may be completely unrelated, and/or the result of noise.

Dr. Denys Glushkov, who is a portfolio manager at Acadian Asset Management, and the former research director at Wharton Research Data Services, as well as a friend of Alpha Architect blog, recently recommended that we read a provocative paper, “Testing Strategies Based on Multiple Signals,” by Novy-Marx, that addresses this issue.

In his paper, Novy-Marx argues that many multi-signal strategies suffer from overfitting bias. Multi-signal strategies often rely on a composite measure that combines multiple signals. Novy-Marx cites some famous examples:

• Piotroski’s F-score (2000) — combines 9 market signals;
• Banker and Wurgler Index (2006) — combines 6 signals of investor sentiment;
• Asness, Frazzini, and Pedersen’s quality score (2013) — combines 21 stock level characteristics..

Novy-Marx distinguishes overfitting bias from selection bias, which occurs when a researcher examines a variety of signals and identifies the best performer, but fails to account for the extent of the search conducted. Under selection bias, a sample of signals tested may be non-random, and thus may require a correction for this bias.

Here is the intuition on how “pure” overfitting and selection biases operate:

1. Pure Selection Bias: A researcher considers many signals, and only reports the best performing signal. The researcher may not report the number of signals tested or the manner in which data were chosen for study, either of which might impart a bias to the results. (see the Harvey, Liu, and Zhu paper for more details)


2. Pure Overfitting Bias: A researcher uses all the signals considered, but optimize for a combination of signals.  Here, the combination is “overfit” to the data examined, and therefore may have no predictive power. Additionally, Novy-Marx observes that researchers may sign the signals (i.e., assign them either a positive or negative directional sign) and/or weight them to predict returns.

Selection bias can magnify the effects of overfitting, in exponential fashion, consistent with a power law. Novy-Marx attempts to measure the interaction and magnitudes of overfitting and selection biases with an experiment.

How do Researchers Test Ideas?

In practice, a research process might involve a researcher considering n signals, and combine the best k of these to select stocks.

If k=1, this may result in pure selection bias.
If k=n, this may result in pure overfitting bias.
If 1 < k < n, the result may be a combination of selection and overfitting.

How Severe are Overfitting and Selection Biases?

If you look at a large sample of signals, some combinations of the signals will perform strongly, just by dumb luck. Novy-Marx makes an amusing analogy: Consider a group of monkeys throwing darts at the stock pages of the Wall Street Journal. Some monkeys will have great performance, and selecting a combination of these monkeys in-sample will yield spectacular performance. Of course, this group will not perform out of sample.

Using real stock data from January 1995 through December 2014, Novy-Marx generates random signals, with none on its own having any power to predict returns.

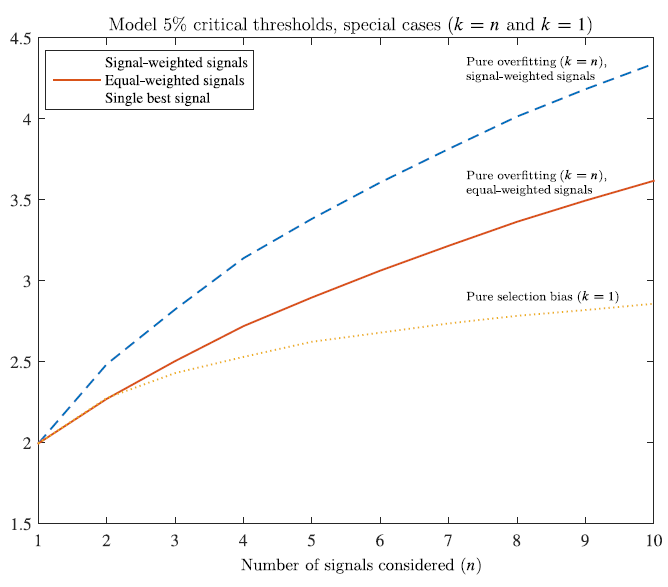
The figure below shows the backtested t-statistics for strategies based on combinations of between 2 and 10 signals:
What do you notice?

• All of these signals have t-value < 2.0 in their individual backtests. So, none of the underlying signals are themselves significant, or have any true predictive power.*
• The bottom yellow dotted line is the strongest result (k) from a set of n random strategies, representing pure selection bias.
• The solid red line equal weights all of the n signals, but signs them (positively or negatively) to predict the strongest in-sample returns, representing pure overfitting.
• The top blue dotted line use all of the n signals, are signed, and are also signal-weighted to maximize returns, representing an even more extreme form of pure overfitting.
• The figure shows that the combined signals are highly significant, with t-value positively correlated with the number of signals used (k).

*t-value measures statistical significance of a t-test. Generally, if a t-value is greater than 2, the estimate is statistically significant at the 5% level. The higher the t-value, the greater the confidence we have in the coefficient as a predictor. Here’s a table of critical values for the t-distribution if you are interested.

Note how in the upper two lines that when the researchers give themselves additional discretion to weigh the signals, the results become more extreme–talk about overfitting!

Selection Bias Equivalence

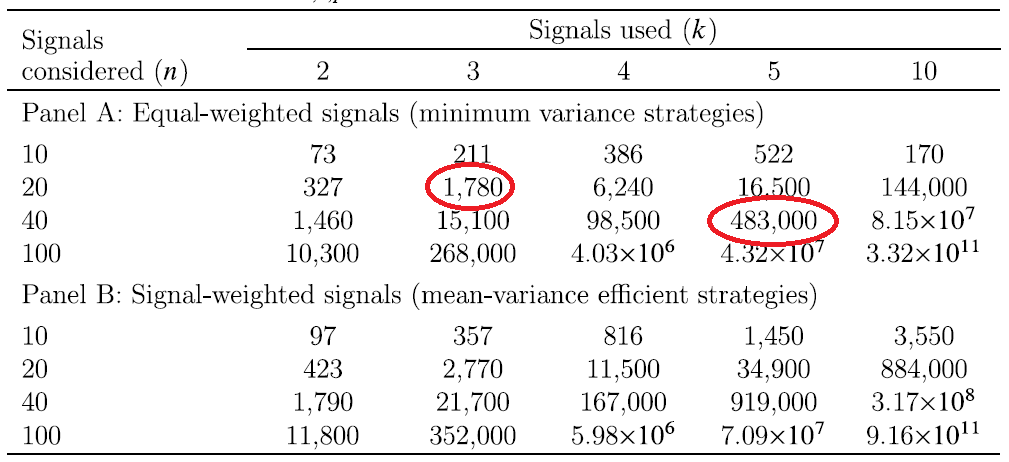
In order to demonstrate how sample selection and overfitting biases can interact with exponential effects, Novy-Marx reports the “selection bias equivalence,” which shows the relationship between selection and overfitting bias. The Table below shows single-signal equivalent sample sizes.

From the paper:

Panel A, which shows the case when multiple signals are equal weighted, shows that using just the best three signals from 20 candidates yields a bias as bad as if the investigator used the single best performing signal from 1,780 candidates. With five signals selected from 40 candidates, the bias is almost as bad as if the investigator had used the single best performing signal from half a million candidates.

Note how in Panel B the selection bias equivalent numbers can get completely crazy. Novy-Marx derives a power law from this relationship. From the paper: “The bias resulting from combining the best k signals from a set of n candidates is almost as bad as that from using the single best signal out of n^k candidates.”

What Are the Implications?

All of this should serve to make you suspicious of any multi-signal strategy you may come across in the market. Why? Because the statistical bar gets very high very fast. Consider a strategy that uses 20 signals. Do you think the people who developed the strategy examined more than 20 signals before coming up with it? You bet they did.

Yet we cannot use conventional statistical tests to evaluate such multi-signal strategies. A great backtest with a strong t-statistic is not really telling you very much.

Novy-Marx suggests some advanced statistical methods to address this issue but also suggests some simplifying rules of thumb. At the very least, you can evaluate multi-signal strategies based on each individual signal, controlling for the fact that the researchers may have investigated many signals.

Calibrating Statistical Significance Based on Sample Size

Say you want to test n signals, and determine the best performer with statistical significance at the 5% level.

If you examine 10 signals, there is a: 1-(1-.05)^10=40% chance of observing a significant result by chance, even if all the signals are insignificant. When you examine 20 signals, there is a: 1-(1-.05)^20=64% chance. As n increases and you examine more and more potential signals, the chance of finding one that is significant due to chance goes higher and higher.

We need a way to adjust our measure of “statistical significance” so that it accounts for this. Novy-Marx suggests the Bonferroni correction, which imposes a higher standard that should apply when we are looking at a large number of n signals. Novy-Marx observes that, “If one suspects that the observer considered 10 strategies, significance at the 5% level requires that the results appear significant, using standard tests, at the 0.5% level.”

Conclusion

Novy-Marx takes pains to point out that he is not suggesting that investors should not use multi-signal strategies. Good standalone signals can be combined in effective ways to make viable composite strategies. He does want to highlight, however, that a great backtest of a combination of signals does not tell you whether the strategy will do well out of sample, or if the individual signals embedded in the multi-signal strategy are any good. And it may be reasonable to conclude from reading this paper that a multi-signal strategy with a lot of signals should be critically evaluated in this light.

Stepping back, thinking about out of sample performance gets even hairier. Consider a situation where we correctly identify a genuine signal in the data using the latest whiz-bang statistical techniques, adjusted for selection bias and overfitting. Does this automatically imply the signals will work out of sample? Unlikely. Markets are highly dynamic and competitive. What if others find out about the signal? Will it be arbitraged away? We recommend all investors answer two basic questions when analyzing a process, be it quantitative or qualitative, and attempt to assess out of sample expected performance:

1. What is the edge and/or risk that drives expected returns?
2. Why isn’t everyone doing it?

Answering these 2 questions will help an investor assess the out-of-sample sustainability of a process, regardless of whether is data-mined or not. A detailed discussion of this high-level framework is discussed in our sustainable active investing framework.

Here is a video lecture on the topic:

Backtesting Strategies Based on Multiple Signals

• Novy-Marx
• A version of the paper can be found here.
• Want a summary of academic papers with alpha? Check out our Academic Research Recap Category.

Abstract:

Strategies selected by combining multiple signals suffer severe overfitting biases, because underlying signals are typically signed such that each predicts positive in-sample returns. “Highly significant” backtested performance is easy to generate by selecting stocks on the basis of combinations of randomly generated signals, which by construction have no true power. This paper analyzes t-statistic distributions for multi-signal strategies, both empirically and theoretically, to determine appropriate critical values, which can be several times standard levels. Overfitting bias also severely exacerbates the multiple testing bias that arises when investigators consider more results than they present. Combining the best k out of n candidate signals yields a bias almost as large as those obtained by selecting the single best of n^k candidate signals.