The Standard and Poor’s (S&P) 500 index is a value-weighted stock index based on the market capitalizations of 500 large companies in the US. This index was introduced in 1957 and intended to be a representative sample of leading companies in leading industries within the US economy. Stocks in the index are chosen for market size, liquidity, and industry group representation. The S&P 500 index appeared as a result of the expansion of the Standard and Poor’s Composite index that was introduced in 1926 and consisted of only 90 stocks.
This index is probably the most commonly followed equity index and many consider it one of the best representations of the US stock market. Many index funds attempt to replicate the performance of the S&P 500 index by holding the same stocks as the index, in the same proportions. The first example of such a fund was the Vanguard Group’s Vanguard 500 that appeared already in 1976. In addition to the index funds, there are exchange-traded funds (ETF) that also replicate the performance of the S&P 500 index.
Because of the widespread popularity of the S&P 500 index, low cost and ease of investing in the S&P 500 index fund, there are lots of studies that investigated the profitability of trend following rules in trading this index. Unfortunately, practically all of these studies used back-tests without correcting for the data-mining bias and ignored such an important market friction as transaction costs. The results of these studies gave birth to lots of myths about the superior performance of trend following trading strategies.
Two examples of such myths are as follows:
- First, one can easily beat the market by using a trend following strategy.
- Second, as compared to its passive counterpart, the trend following strategy has greater returns with lower risk. So there is no downside in implementing the trend following strategy.
In other words, you can have your cake and eat it too.
We, on the other hand, use a forward-testing methodology, account for realistic transaction costs, and comprehensively evaluate the profitability of various trend following rules in trading the S&P 500 index. The results of this study allow us to revisit the myths regarding the superior performance of the trend following rules in this well-known stock market and fully understand their advantages and disadvantages.
The Structure of Our Trend-Following Tests
In our tests we use the following 5 trend following rules: MOM, P-MA, MAC, MAE, and MACD. We estimate the profitability of each single rule and the combined rule (COMBI). In the combined rule, the performance of each single trading rule is evaluated in the in-sample segment of data; then the best trading rule is selected and its returns are simulated in the out-of-sample segment of data. See Part 6 of this blog series for the detailed description of the forward testing procedure.
Note that a practical realization of 4 out of 5 single rules requires choosing a particular moving average (SMA, LMA, EMA, etc). In addition, when a trading rule generates a Sell signal, there are two possible actions: either move to cash or sell short the stocks. Finally, because there are several alternative performance measures, the selection of the best trading strategy may depend on the choice of performance measure. To reduce the dimensionality of testing procedure, first of all we conduct a few minor studies to answer the following questions: Does the choice of performance measure influence the selection of the best trading strategy? Does the choice of moving average influence the performance of the best trading strategy? Is it sensible to consider the strategy with short sales?
The results of these studies allow us to make the following conclusions:
- The short selling strategy is risky and does not pay off. Specifically, the performance of the short selling strategy is substantially worse than the performance of the corresponding strategy where the trader switches to cash (or stays invested in cash) after a Sell signal is generated. The reason for the poor performance of the short selling strategy is that a trend following rule identifies the direction of a trend with far from perfect accuracy;
- From a practical point of view, the choice of performance measure does not influence the ranking of trading strategies. When the performance is measured using either daily or monthly returns, all performance measures produce virtually identical ranking of trading strategies. Therefore the Sharpe ratio, which has become the industry standard for measuring risk-adjusted performance, is superior to other performance measures from a practitioner’s point of view;
- From a practical point of view, the choice of moving average does not have a crucial influence on the performance of trend following strategies. In particular, regardless of the choice of moving average, the performance of the best trading strategy remains virtually intact. In this regard, the SMA can be preferred as the simplest, best known and best understood moving average. Note that our analysis of the properties of ordinary moving averages (see Part 2 of this blog series) suggested that, theoretically, LMA and EMA might have some potential advantages over SMA. Unfortunately, in practical applications these advantages are not realized.
We remind the reader that, even though forward-tests are supposed to be purely objective tests that allow the trader to evaluate the true profitability of a trading rule, in reality the outcome of a forward test depends generally on the choice of a historical period and on the choice of split point between the in-sample and out-of-sample segment of data (see Part 6 of this blog series). This fact gives the possibility to manipulate the results of a forward test. In particular, the choice of the historical period and/or the split point can be a decisive factor that determines whether or not a trend following strategy outperforms its passive counterpart.
In our forward tests we use monthly data from January 1926 to December 2015; January 1950 is used as the split point between the in-sample and out-of-sample segment of data. Our choices are motivated by the following considerations. First, even though the data for the S&P Composite index can be extended back in time to 1800, the post-1926 data are more reliable than the pre-1926 data. Second, we identified the presence of a major structural break around year 1944 in the growth rate of the index. Therefore the historical profitability of trend following rules after the break can be used as a reliable indicator of their future profitability. Still, there are multiple choices to select the split point. Depending on the choice of the split point, the p-value of the outperformance test can vary from virtually 0% to almost 100%. However, our analysis reveals that for the majority of choices the p-value of the outperformance tests lies in between 15% and 25%. So using January 1950 as the split point guarantees a long out-of-sample period with many bull and bear markets and produces a typical estimate of historical outperformance and its statistical significance.
When we simulate the returns to a trend following strategy, we impose 0.25% one-way transaction costs (assuming that the transaction costs are proportional to the volume of trading).
Our Core Trend-Following Results
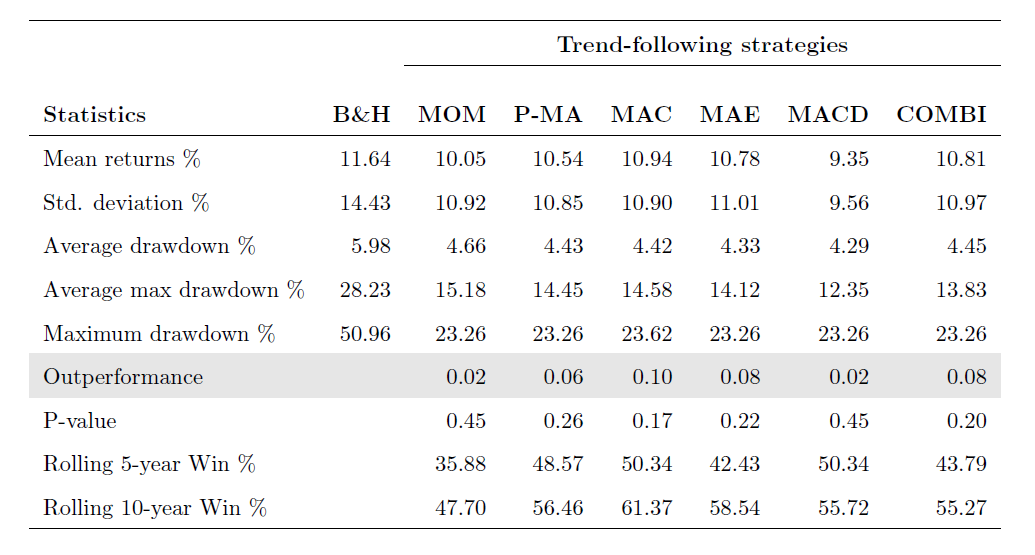
The table below reports the descriptive statistics of the buy-and-hold strategy (denoted by B&H) and the out-of-sample performance of the trend following strategies. First of all, we focus on the estimated mean returns and standard deviation of returns; both of these estimates are annualized and reported in percentages. Note the following. Judging by the values of the standard deviation of returns (which is the common risk measure in modern finance theory), all trend following strategies are virtually equally risky. We observe a significant reduction in risk as compared to the riskiness of the passive strategy. However, the reduction of risk is not surprising because virtually in any trend following strategy about 1/3 of the time the money is held in cash. The mean returns to the trend following strategies are also below the mean returns to the passive strategy. Thus, the trend following strategy has both lower returns and risk as compared to those of its passive counterpart.
The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request.
Second, we focus on the estimated outperformance which is measured by Δ=SRTF-SRBH, where SRTF and SRBH denote the Sharpe ratios of the trend following and buy-and-hold strategy respectively. The Sharpe ratios are annualized; the p-value of the outperformance test is reported below the value of the estimated outperformance. Recall that the Sharpe ratio can be computed as
![Rendered by QuickLaTeX.com SR_i = \frac{E[r_i]-E[r_f]}{\sigma_i},](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%20135%2028'%3E%3C/svg%3E)
where E[ri] and E[rf] are the mean returns to strategy i and the mean returns to the risk-free asset respectively, and σi is the standard deviation of returns to strategy i. Over the out-of-sample period, the mean value of the risk-free rate of return equals 4.35%. Consequently, the Sharpe ratio of the buy-and-hold strategy equals (11.64-4.35)/14.43=0.50. For example, the Sharpe ratio of the MAC strategy equals (10.94-4.35)/10.90=0.60. Therefore, the outperformance generated by the MAC strategy amounts to 0.60-0.50=0.10.
Note that judging by the estimated outperformance, every single trend-following strategy and the combined strategy outperforms the buy-and-hold strategy on the risk-adjusted basis. However, none of the trend following strategies statistically significantly outperforms the buy-and-hold strategy at conventional statistical levels (1%, 5%, and 10%). The median p-value of the outperformance test is about 25%. This value means that there is approximately 25% probability that the Sharpe ratio of the buy-and-hold strategy is greater than the Sharpe ratio of the trend following strategy.
In addition to the standard deviation of returns, the following risk measures are reported: the maximum drawdown, the average maximum drawdown which is an equally-weighted average of the 10 largest drawdowns, and the average drawdown. The advantage of the trend following strategy is more pronounced when one compares the drawdown-based measures of risk of the trend following strategy and the corresponding buy-and-hold strategy. Over the total out-of-sample period, whereas the reduction of standard deviation amounts to approximately 1/3, the reduction of the maximum drawdown and the average maximum drawdown amounts to approximately 1/2. That is, a trend following strategy reduces drawdowns much more effectively than it reduces the variability of returns (measured by standard deviation). Therefore, in our opinion, the main advantage of the trend following strategy lies in its ability to limit the potential losses. That is, the trend following strategy is a strategy with downside protection.
The figure below, upper panel, plots the cumulative returns to the buy-and-hold strategy and the MAC strategy simulated out-of-sample. The lower panel in this figure plots the drawdowns to the buy-and-hold strategy and the MAC strategy. It is worth noting that, over the 65-year long out-of-sample period, the cumulative return to the trend following strategy is slightly less than that of the buy-and-hold strategy. Yet, the trend following strategy is substantially less risky. We will elaborate more on this property of the trend following strategy at the end of this blog post.

The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request.
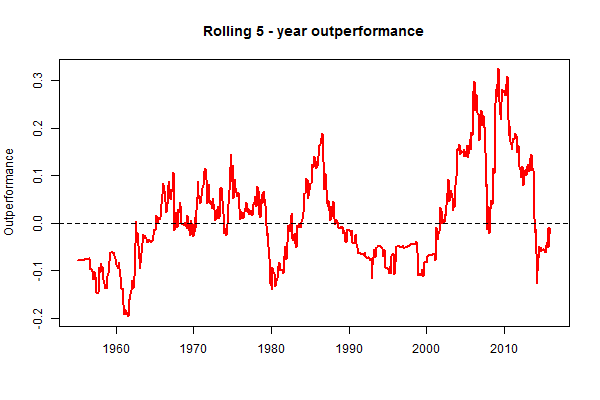
A very prominent feature of the outperformance generated by a trend following strategy is that it is very uneven over time. As a rule, a trend following strategy underperforms its passive counterpart during bull markets and outperforms during bear markets. This is because a trend following strategy identifies the direction of a trend with about 75% accuracy; that is, a correct trading signal is generated about 3/4 of the time. As a result, during bull markets a trend following strategy generates a series of false Sell signals. These wrong Sell signals deteriorate the performance of a trend following strategy during bull markets. During bear markets a trend following strategy generates a series of false Buy signals. However, if a bear market is rather long, a trend following strategy provides protection from losses even in the presence of some false Buy signals.
To illustrate the uneven outperformance generated by a trend following strategy, the figure below shows the rolling 5-year outperformance produced by the MAC strategy simulated out-of-sample. Specifically, the first point in this plot shows the outperformance over a 5-year period from January 1950 to December 1954; the second point shows the outperformance over a 5-year period from February 1950 to January 1955; etc. The plot in this figure clearly demonstrates that the outperformance is not only highly non-uniform over time, but often a trend following strategy underperforms its passive counterpart. Therefore the reported (in the table above) outperformance is a measure of average outperformance computed using a very long-run horizon (note that this horizon is beyond the investment horizon of any individual investor). Since the majority of investors have short- to medium term horizons, the average outperformance produced by a trend following strategy over a horizon of 65 years is not especially relevant. In order to provide a more accurate picture of outperformance, using rolling windows of 5 and 10 years, in the table above we report the probability that the trend following strategy outperforms its passive counterpart over an arbitrary historical period of 5 and 10 years. These probabilities are denoted as “Rolling 5(10)-year Win %.” Observe that over a 5-year horizon the probability that a trend following strategy outperforms its passive counterpart is less than 50%. That is, over a 5-year horizon a trend following strategy is more likely to underperform than to outperform the buy-and-hold strategy. However, the probability of outperformance increases as the investment horizon increases.
The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request.
Does Trend-Following Beat Buy and Hold?
The ultimate question we are trying to answer is this one: Does the trend following strategy outperforms the buy-and-hold strategy?
To answer this question, using the past data and the forward-testing methodology we evaluated the outperformance delivered by the trend-following strategy and tested whether the outperformance is statistically significant.
Here is a brief summary of our results so far:
- The outperformance produced by the trend-following strategy tends to be positive over a long run. However, this outperformance is not statistically significant at conventional statistical levels. Therefore the results of our tests are encouraging, but inconclusive;
- The trend-following strategy tends to underperform (outperform) the buy-and-hold strategy during bull (bear) markets;
- The outperformance is very uneven in time and is not guaranteed. In fact, our results suggest that over short- to medium-term horizons the trend following strategy is more likely to underperform the market than to outperform;
- The trend following strategy has lower mean returns and lower standard deviation of returns than those of the buy-and-hold strategy. Thus, and it is very important to emphasize, the trend following strategy is not a “high returns, low risk” strategy as compared to the buy-and-hold strategy. In reality, it is a “low returns, low risk” strategy;
- The main advantage of the trend-following strategy seems to be its ability to limit the potential losses.
However, even though in our tests we used the contemporary “state of the art” performance measurement methodology that is employed in the papers published in the leading financial journals, one has always to keep in mind that the performance measurement theory is based on a number of assumptions that are usually not met in reality. Another deficiency of the standard performance measurement methodology employed in modern finance is that one uses exclusively high-frequency data (asset returns sampled at the daily or monthly frequency). If the investor invests for a long term, it makes much more sense to use low-frequency data. That is, to use asset returns sampled at a multi-year frequency. However, in this case the number of independent return observations happens to be very low and, consequently, statistical tests have very low power. Still, it is exceedingly insightful to demonstrate the difference in probability distributions of the returns to the trend following and buy-and hold strategies sampled at low frequencies.
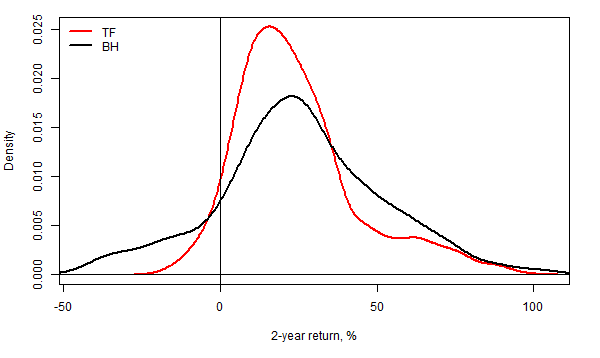
For this purpose, we compound (that is, aggregate) the monthly returns to the MAC strategy simulated out-of-sample and the corresponding buy-and-hold strategy to returns over 2-year periods. The figure below plots the empirical probability distribution functions of 2-year returns to the buy-and-hold strategy and the trend-following strategy. This figure advocates that the shapes of the two empirical probability distribution functions are rather different. Specifically, whereas the probability distribution function of 2-year returns to the buy-and-hold strategy has almost symmetrical shape around the mean, the probability distribution function of 2-year returns to the trend-following strategy has a distinct right-skewed shape. It is important to observe that the two empirical probability distribution functions differ mainly in the domain of losses where the returns are negative. In contrast, in the domain of gains where the returns are positive, the two distribution functions differ only a little. Since the probability of loss equals the area under the probability distribution function to the left of zero, we conclude that the probability of losing money over a 2-year horizon is much higher for the buy-and-hold strategy than for the trend-following strategy.
The shapes of the two empirical probability distribution functions suggest that, when we compare the riskiness of the two alternative strategies using the standard deviation, we compare “apples and oranges.” A correct comparison of riskiness requires taking into account the differences between the shapes of the two probability distribution functions. To provide a deeper insight into the comparative riskiness of several alternative strategies, in addition to the standard deviation we will also compute the skewness of the probability distribution and the probability of loss. Formally, the probability of loss is defined by

where r denotes the return and Prob(.) denotes the probability. The problem in using the probability of loss as a risk measure is the fact that this measure tells nothing about the magnitude of potential loss if loss occurs. That is, in principle, one financial asset may have a higher probability of loss than the other asset, but the losses on the latter asset might be much more severe than the losses on the former asset. To complete the picture of losses, we will also compute the expected loss if loss occurs. This risk measure represents a specific realization of the popular risk measure that is known under different aliases: the Conditional Value-at-Risk (CVaR), the Expected Shortfall (ES), and the Expected Tail Loss (ETL). Formally, the expected loss if loss occurs is computed as
![Rendered by QuickLaTeX.com \text{Expected loss if loss occurs}= -E[r|r<0],](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%20331%2019'%3E%3C/svg%3E)
where E[r|r<0] denotes the expected return conditional on the outcome r<0.
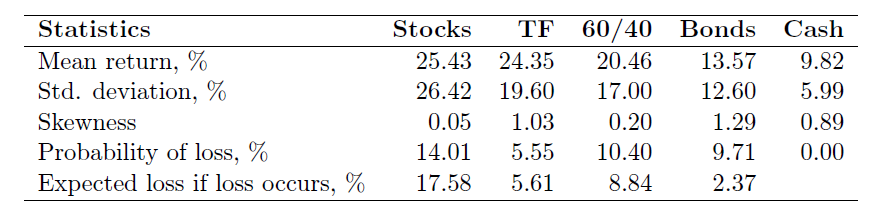
Besides the descriptive statistics of 2-year returns to stocks (that is, the buy-and-hold strategy) and the trend-following strategy, we compute the descriptive statistics of 2-year returns to bonds, cash, and the 60/40 portfolio of stocks and bonds. The bonds return is an equally-weighted return on the long- and intermediate-term US government bonds. The 60/40 portfolio of stocks and bonds is popular with pension funds and other long-term investors. This portfolio mix represents the “rule of thumb” for retirement portfolios. The 60/40 portfolio mix also serves as a benchmark in most portfolio discussions.
The table below reports the descriptive statistics of 2-year returns for the three major asset classes as well as the descriptive statistics for the trend-following strategy and the 60/40 portfolio mix. These 2-year returns are aggregated monthly returns over the period from January 1950 to December 2011. The assets in the table are ordered left-to-right by decreasing mean returns and standard deviation of returns.
Observe that the trend-following strategy is located in between the stocks and the 60/40 portfolio mix. This is because the trend-following strategy has lower mean return than that of the stocks, but higher mean return than that of the 60/40 portfolio mix. Similarly, the trend-following strategy has lower standard deviation of returns than that of the stocks, but higher standard deviation of return than that of the 60/40 portfolio mix. That is, judging by the mean-variance criterion, the trend-following strategy is more rewarding than the 60/40 portfolio mix, but at the same time it is more risky.
The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request.
On the other hand, when risk is measured by the probability of loss and expected loss, the trend-following strategy proves to be less risky than the 60/40 portfolio mix. In other words, if we define risk as the chance of a negative outcome, then the trend-following strategy is both more rewarding and less risky than the popular retirement portfolio. The fact, that the trend-following strategy has higher standard deviation than that of the popular portfolio mix, appears mainly because the trend-following strategy has higher variability (as compared with the 60/40 portfolio) in the domain of gains, which has nothing to do with riskiness. Interestingly, the trend-following strategy has lower probability of loss than that of bonds. However, as revealed by the expected loss risk measure, losses on the trend-following strategy tend to be more severe as compared with losses on bonds. Finally note that, even though the cash plays the role of the risk-free asset in modern finance theory, over a 2-year horizon the cash is clearly a risky asset if risk is measured by standard deviation. Specifically, the standard deviation of 2-year returns on cash amounts to about 6% which is about twice as low as that of bond returns. In contrast, when risk is measured by the probability of loss, the cash remains a risk-free asset.
Compared to the passive investment in stocks, the trend-following strategy has a bit lower mean return, but at the same time substantially lower risk that is measured by the probability of loss and expected loss. In particular, the trend-following strategy has approximately thrice as low the probability of loss and the expected loss as that of the buy-and-hold strategy. Even though the long-run growth from investing in stocks exceeds the long-run growth provided by the trend-following strategy, over short- to medium-term horizons the trend-following strategy is much less risky than the buy-and-hold strategy. Therefore the trend-following strategy appeals not only to risk averse investors who invest for a long-run, but also to less risk averse investors who invest for a medium-run. As compared to the popular 60/40 portfolio mix, the trend-following strategy seems to have a superior reward-to-risk combination. Thus, the trend-following strategy seems to be a better retirement portfolio than the 60/40 portfolio.
Last but not least, the returns to the trend-following strategy resemble the returns to a popular “portfolio insurance” strategy. In particular, traditional portfolio insurance strategy consists of investing in stocks and buying put options on stocks as insurance. The price of these put options represents, in fact, the insurance premium the investor pays to buy portfolio insurance. During bull markets when stock prices trend upward, the insurance premium represents a cost that reduces the investor’s return. However, during bear markets when stock prices trend downward and the investor loses on the stocks, the portfolio insurance covers a part of the losses. As a result, the portfolio insurance strategy underperforms the buy-and-hold strategy during bull markets, but outperforms the buy-and-hold strategy during bear markets. Similarly, we found that the trend-following strategy tends to underperform (outperform) the buy-and-hold strategy during bull (bear) markets. In contrast to the traditional portfolio insurance strategy, in the trend-following strategy eventual losses on the stocks are “covered” only partially, and the amount of covered losses varies over time. Anyway, the trend-following strategy represents a prudent investment strategy for a risk averse investor (or as a retirement portfolio) because its mean return and risk are reasonably consistent with his objectives and risk tolerance.
Our Assessment of Trend-Following Strategies
To sum up, the results of our study allow us to debunk some myths about the superior performance of the trend following strategy. First, as compared to the buy-and-hold strategy, the trend following strategy does not have greater returns with lower risk. It has lower returns with lower risk. Second, it is not easy to beat the market by using a trend following strategy. In fact, there is absolutely no statistical evidence that the trend following strategy outperforms its passive counterpart. However, our results do not indicate that trend following strategies are worthless. On the contrary, our results reveal that a trend following strategy does possess some important advantages over the buy-and-hold strategy. These advantages consist in lower riskiness and downside protection.
We remind the reader (see Part 5 of this blog series) that the justification of the Sharpe ratio, as well as any other rational reward-to-risk performance measure, is based on the assumption a risk-free asset exists. This assumption is convenient because facilitates the unique choice of the theoretically “best” risky portfolio for all investors. However, this assumption is not met in reality. If we relax this assumption, then all modern finance theory says is that the choice of the best risky asset or portfolio depends on the investor’s risk aversion. In our context, the investor faces the choice between investing either in the S&P 500 index or in the trend following strategy that switches between the S&P 500 index and the cash depending on the identified trend direction. Finance theory says that, in the absence of the risk-free asset, risk tolerant investors tend to choose the S&P 500 index, whereas risk averse investors tend to prefer the trend following strategy.
In making this crucial decision (which strategy to follow), the investor has to decide what is the most relevant risk measure, how long is the expected investment horizon, and in addition answer the following question: Am I a defensive or an aggressive investor? In our opinion, the buy-and-hold strategy is suitable for a long-term aggressive investor only. If the investor is of the defensive type, or the investment horizon is either short-term or medium-term, the investor should choose the trend following strategy. But keep in mind that in this case the investor can be often disappointed because the trend following strategy lags behind the buy-and-hold strategy when the stock market trends upward during a bull market. In return, the trend following strategy is able to protect the investor from huge losses during a severe bear market.
Additional Resources for Self-Study
Even though, in our opinion, the performance of trend-following rules in back-tests cannot be used as a reliable estimate of the expected future performance of these rules, the interested reader can conduct back-tests of different trend-following rules is various stock markets. For this purpose we provide these interactive web illustrations. These illustrations allow one to select the stock market data, the in-sample period, the trading rule, the type of moving average, the amount of transaction costs, the performance measure, etc. In-sample tests are very fast and, therefore, the reader can immediately see the results of in-sample tests reported in several panels.
The performance of trend-following rules in forward-tests is much more interesting and relevant. We provide interactive resources to conduct forward-tests of trend-following rules. But keep in mind that forward (i.e. out-of-sample) tests are much more time consuming than in-sample tests. Therefore, please be patient after selecting the required data source and other test parameters (especially when the combined rule is tested).
Here is a link to our trend-following series.
About the Author: Valeriy Zakamulin
—
Important Disclosures
For informational and educational purposes only and should not be construed as specific investment, accounting, legal, or tax advice. Certain information is deemed to be reliable, but its accuracy and completeness cannot be guaranteed. Third party information may become outdated or otherwise superseded without notice. Neither the Securities and Exchange Commission (SEC) nor any other federal or state agency has approved, determined the accuracy, or confirmed the adequacy of this article.
The views and opinions expressed herein are those of the author and do not necessarily reflect the views of Alpha Architect, its affiliates or its employees. Our full disclosures are available here. Definitions of common statistics used in our analysis are available here (towards the bottom).
Join thousands of other readers and subscribe to our blog.