“From shirtsleeves to shirtsleeves in three generations.”
– Andrew Carnegie
Since time immemorial, humans have wondered at the factors that give rise to the accumulation of wealth. Why do some people seem to have a knack for generating wealth, while others seem to have a knack for bankruptcy? Some recent neuroeconomics research sheds some light on this subject, and suggests that differences between individuals may play a larger role than was previously thought.
Many now believe that humans possess two distinct brain regions, each with its own cognitive system, that deal with 1) excitement around potential gains, such as before we make a risky bet in a vegas casino, and 2) anxiety around potential losses, such as when we turn down such a risky bet. Indeed, MRI brain imaging has shown independent patterns of neural activity when the brain anticipates gains versus when it anticipates losses.
One interesting aspect of these two systems is that individuals might generate more cognitive activity and be able to learn faster in one system versus the other, and this could have some implications for their life financial outcomes.
In “Gain and loss learning differentially contribute to life financial outcomes” Knutson, Samanez-Larkin, and Kuhnen devised an ingenious test to measure and assess how well people learn in gain and loss conditions. Subjects were given a series of learning tasks using fractal cues. “What kind of learning task, and what the hell is a fractal cue” you ask? The outcome is so strange, it is worth taking a moment to understand the test.
Ok, so you will recall what a fractal is:
In order to perform the test, the researchers created three different pairs of such fractals; we’ll call them Pair X, Pair Y and Pair Z. In each trial, subjects were presented with one of these three pairs of fractals, and then asked to choose one of the two fractals making up the pair. Different choices yielded different payoffs.
Here’s how the payoffs worked.
The first pair, Pair X, was a “gain” pair, consisting of Fractal A and Fractal B. In the gain pair, choosing Fractal A resulted in a 66% probability in a gain of $1, while choosing Fractal B resulted in a 33% probability of a gain of $1.
The second pair, Pair Y, was a “loss” pair, consisting of Fractal C and Fractal D. In the loss pair, choosing Fractal C resulted in a 66% probability of losing $1, while choosing Fractal D resulted in a 33% probability of a loss of $1.
The third pair, Pair Z, was a “neutral” pair. In the neutral pair, there were never any gains or losses.
Let’s walk through an example.
Let’s say the example above is Pair X, the “gain” pair. The subject is asked to choose between the blue fractal in the first box, and the green fractal in the second box. Let’s say the blue fractal is Fractal A. With Fractal A, he wins $1 66% of the time. In the case above a subject chooses “blue,” Fractal A, and wins $1.
A little while later, the subject will see Pair X again, and this time he might choose the green fractal, or Fractal B. With Fractal B he only wins 33% of the time, so let’s say he wins $0. “Hmmm,” says the subject. “I won $1, when I chose blue, but didn’t win anything when I chose green. That’s interesting.”
Now sometimes blue is not going to win, and sometimes green will win, but over time, as the subject sees Pair X over and over again, and gets to see the outcome of more and more of his choices, it is going to dawn on him that he wins more often when he picks blue. Thus, the subject learns the optimal or correct choice to maximize his gains: blue.
Now flip this logic over to the Pair Y, or the “loss” pair. In the same way as above, the subject will gradually learn how to minimize his losses.
It turns out some people are very good at quickly figuring out that when they see Pair X, they should choose blue. They are good at gain learning, and scored a high % of correct choices for Pair X gain choices. Likewise, some people are very good quickly determining how to avoid the bigger losses associated with the wrong choice with Pair Y. These subjects are good at loss learning, and scored a high % of correct choices for Pair Y loss choices. Again, this learning appears to be taking part in different areas of the brain.
Now here’s the interesting part.
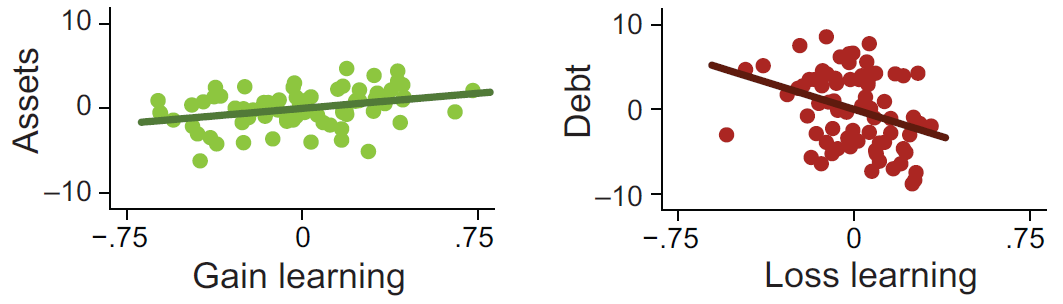
The researchers also collected financial data on the study subjects. In particular, the researchers assessed the subjects’ assets (e.g., portion of home owned, bank accounts, investments) and debts (e.g., home loans, car loans, student loans).
Next they regressed the relationships between the learning variables (gain % of correct choices, loss % of correct choices, etc.) and these life financial outcomes of assets and debt. The thinking was the gain learning might promote asset accumulation, while loss learning might promotes debt avoidance.
Here are the results of the regression:
As the Turnkey PhD would say, “holy snikes!” It appears that there is a strong correlation between 1) gain learning and asset accumulation, and 2) loss learning and lower levels of debt! Those neuroeconomic academics come up with the most astounding observations, don’t they? How might we apply these results in the real world?
Let’s say you took a test indicating you have a weakness in gain learning. Your financial advisor might be able to then say to you, “given your profile on this test, you may underweight risky assets, so let’s look critically at your asset allocation.” Or maybe you have a weakness in loss learning, and your financial advisor might say, “Since you are considering getting an advanced degree, let’s focus on the required student loans in light of your overall credit situation.”
Perhaps a particular differential creates distinct biases to watch out for: you’re very strong in gain learning and have a diversified investment portfolio, but weak in loss learning, with the result that you periodically take on too much margin debt for your age.
Ok, well maybe I’m getting carried away here, but certainly this concept might reasonably apply to some obvious, basic financial areas such as one’s savings rate, or how to finance a car. It could also be that these biases extend into many additional not-so-obvious areas: career choices, where you live, retirement and estate planning. I for one cannot wait to see how this fascinating branch of neuroeconomic and behavioral research evolves.
About the Author: David Foulke
—
Important Disclosures
For informational and educational purposes only and should not be construed as specific investment, accounting, legal, or tax advice. Certain information is deemed to be reliable, but its accuracy and completeness cannot be guaranteed. Third party information may become outdated or otherwise superseded without notice. Neither the Securities and Exchange Commission (SEC) nor any other federal or state agency has approved, determined the accuracy, or confirmed the adequacy of this article.
The views and opinions expressed herein are those of the author and do not necessarily reflect the views of Alpha Architect, its affiliates or its employees. Our full disclosures are available here. Definitions of common statistics used in our analysis are available here (towards the bottom).
Join thousands of other readers and subscribe to our blog.