Factor analysis has taken the professional consultant world by storm and we are slowly seeing this analysis being used more and more by sophisticated retail investors and investment advisors. And that’s great–factor analysis is a great tool. In fact, we discuss the use of the tool and how it is useful in a recent post called, Basic Factor Analysis: Simple Tools to Understand What Drives Performance.
But factor analysis is not an end-all, be-all. There are other considerations for evaluating strategies. One should use multiple tools–all the time–when analyzing the performance of a strategy/process.
We outline the pitfalls of factor analysis in one of our working papers on maximum drawdowns. The basic idea is that preservation is paramount in investing. This is fairly obvious, as an investor can’t compound $0. But if it is so obvious, why do most performance assessment discussions focus on statistics that do a poor job capturing tail risk?
Consider the concept of “alpha,” which is simply the intercept estimate from a linear regression with a bunch of ‘factors’ that are meant to control for risk exposures. As the story goes, if a manager has a positive alpha, after controlling for factor exposures, they’ve got a lot of skill. So should we just look for alpha in isolation from other considerations? No.
Where does this analysis go awry?
In Table 1 we highlight with a simple example why tail risk requires researcher attention. Table 1 shows a set of statistical measures included in many academic anomaly papers: average monthly returns, standard deviation of returns, and a laundry list of linear factor model alphas. We analyze 3 time series: 1) the value-weight CRSP index, 2) the value-weight CRSP index with 10 percent alpha injected (we simply add 10%/12 into each monthly return), and 3) the value-weight CRSP index with a 10 percent alpha injection, but the index experiences a final return of -100%, or in other words, the index goes bankrupt.
Table 1: Summary Statistics for Hypothetical Alpha Portfolio
| VW CRSP | VW CRSP w/alpha | VW CRSP w/alpha & Bankruptcy | |
| Average monthly returns | 0.0088 | 0.0171 | 0.0154 |
| Standard dev. (monthly) | 0.0450 | 0.0450 | 0.0614 |
| 1-Factor alpha | -0.0001 | 0.0082 | 0.0065 |
| 0.0000 | 0.0000 | 0.0001 | |
| 3-Factor alpha | -0.0001 | 0.0082 | 0.0069 |
| 0.0000 | 0.0000 | 0.0000 | |
| 4-Factor alpha | -0.0001 | 0.0082 | 0.0067 |
| 0.0000 | 0.0000 | 0.0000 |
This table reports calendar-time portfolio regression alphas and summary statistics for the value-weight CRSP index (VW CRSP), the VW CRSP index with 10% alpha (we add 10%/12 to each monthly return), and the VW CRSP with 10% alpha and a final monthly return of -100% (VW CRSP w/ alpha & bankruptcy). Portfolios for each strategy are rebalanced each year on July 1st and are held from July 1st of year t until June 30th of year t+1. The time period under analysis is from July 1, 1963, to December 31, 2012. For each portfolio (column), we show the average monthly return and the standard deviation of the monthly returns. We calculate monthly returns to the portfolios and run regressions against linear factor models. The four factors are: the return on the stock market (MKT), the return spread between small and large stocks (SMB), the return spread between stocks with high and low book-to-market ratios (HML), and the spread between high and low momentum stocks (UMD). We get the monthly factor returns from Ken French’s website. We regress the monthly portfolio returns against the 1-factor model (MKT), the 3-factor model (MKT, SMB, and HML), and the 4-factor model (MKT, SMB, HML, UMD). Monthly Alphas are calculated, with p-values below the coefficient estimates, and 5% statistical significance is indicated in bold. All p-values use robust standard errors as computed in Davidson and MacKinnon (1993, 5. 553). The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request.
The alpha estimates for the alpha injected series and the alpha injected series with an eventual bankruptcy are robust and highly significant alphas across all factor models. The author of this research study would proclaim that investing in an eventual bankrupt, high-alpha value-weight CRSP index rejects the market efficiency hypothesis.
Yet, because the strategy goes bankrupt, by definition it cannot have created any alpha and thus this outcome would seem to be consistent with the efficient market hypothesis, i.e., you can’t beat the market.
Here is a visual depiction of the invested growth of these various portfolios:
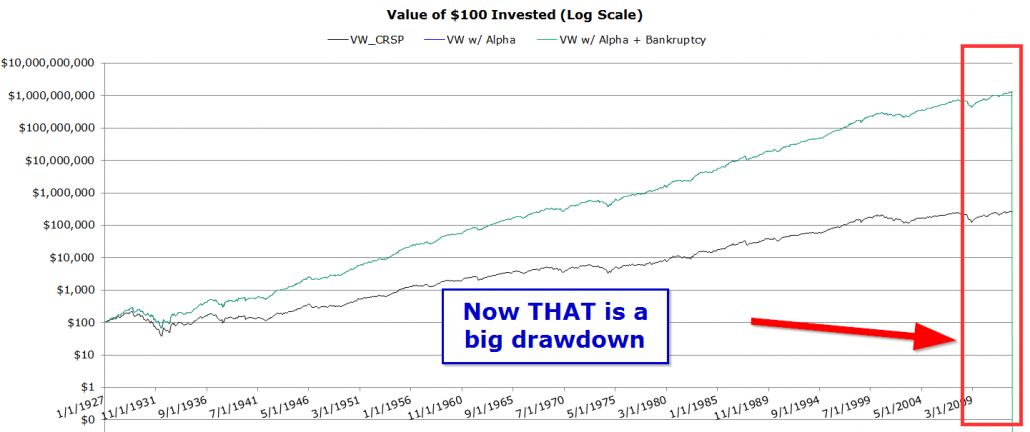
The results are hypothetical results and are NOT an indicator of future results and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request.
The reality is that researchers need to include measures of tail risk for a particular strategy before claiming an anomaly victory.
Bottomline: Factor model statistics don’t tell us everything.
We’ll leave the last word to Warren Buffett:
Academics, however, like to define investment “risk” differently, averring that it is the relative volatility of a stock or portfolio of stocks – that is, their volatility as compared to that of a large universe of stocks…Employing data bases and statistical skills, these academics compute with precision the “beta” of a stock – its relative volatility in the past – and then build arcane investment and capital-allocation theories around this calculation…
Buffett then throws mud in the face of anyone focused on classic volatility (i.e., standard deviation)
In fact, the true investor welcomes volatility.
About the Author: Wesley Gray, PhD
—
Important Disclosures
For informational and educational purposes only and should not be construed as specific investment, accounting, legal, or tax advice. Certain information is deemed to be reliable, but its accuracy and completeness cannot be guaranteed. Third party information may become outdated or otherwise superseded without notice. Neither the Securities and Exchange Commission (SEC) nor any other federal or state agency has approved, determined the accuracy, or confirmed the adequacy of this article.
The views and opinions expressed herein are those of the author and do not necessarily reflect the views of Alpha Architect, its affiliates or its employees. Our full disclosures are available here. Definitions of common statistics used in our analysis are available here (towards the bottom).
Join thousands of other readers and subscribe to our blog.

